Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
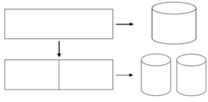
Gọi R và r lần lượt là bán kính đáy của mỗi thùng đựng nước hình trụ được làm theo cách 1 và cách 2.
Gọi C1 và C2 lần lượt là chu vi đáy của mỗi thùng đựng nước hình trụ được làm theo cách 1 và cách 2.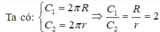
(vì cắt tấm tôn ban đầu thành hai tấm bằng nhau nên C1 = 2C2)
Thùng làm theo cả hai cách đều có cùng chiều cao h nên ta có:
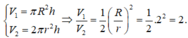

Ta có tứ diện đều ABCD, M là một điểm trong của nó. Gọi V là thể tích, S là diện tích mỗi mặt của tứ diện đều ABCD, h A , h B , h C , h D lần lượt là khoảng cách từ M đến các mặt (BCD), (CDA), (DAB), (ABC).
Khi đó ta có:
V = V MBCD + V MCDA + V MDAB + V MABCV
= S( h A + h B + h C + h D )/3
Từ đó suy ra h A + h B + h C + h D = 3V/S

Có thể đưa về hàm số:
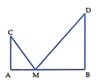
\(AB=2\Rightarrow MB=\sqrt{AB^2-MA^2}=\sqrt{4-MA^2}\)
Đặt \(MA=t\) với \(0\le t\le2\) \(\Rightarrow MB=\sqrt{4-t^2}\)
\(P=MA+2MB=f\left(t\right)=t+2\sqrt{4-t^2}\)
Xét hàm \(f\left(t\right)\) trên \(\left[0;2\right]\)
\(f'\left(t\right)=1-\dfrac{2t}{\sqrt{4-t^2}}=0\Rightarrow2t=\sqrt{4-t^2}\Rightarrow5t^2=4\Rightarrow t=\dfrac{2}{\sqrt{5}}\)
\(f\left(0\right)=4\) ; \(f\left(2\right)=2\) ; \(f\left(\dfrac{2}{\sqrt{5}}\right)=2\sqrt{5}\)
\(\Rightarrow f\left(t\right)_{max}=2\sqrt{5}\Rightarrow P_{max}=2\sqrt{5}\)
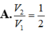

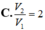




cách cô giáo đùng