Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

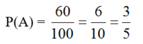
a) Không gian mẫu là kết quả của việc lấy ngẫu nhiên 1 quả cầu ở hộp thứ nhất và một quả cầu ở hộp thứ hai
+ Có 10 cách lấy 1 quả cầu bất kì ở hộp 1 và có 10 cách lấy 1 quả cầu bất kì ở hộp 2. Nên số phần tử của không gian mẫu là;
⇒ n(Ω) = 10.10 = 100.
A: “ Quả cầu lấy từ hộp thứ nhất trắng”
⇒ Có 6 cách lấy quả cầu màu trắng ở hộp A và 10 cách lấy quả cầu ở hộp B
⇒ n(A) = 6.10 = 60.
B: “Quả cầu lấy từ hộp thứ hai trắng”
⇒ Có 4 cách lấy quả cầu màu trắng ở hộp B và 10 cách lấy quả cầu ở hộp A
⇒ n(B) = 4.10 = 40.
A.B: “Cả hai quả cầu lấy ra đều trắng”
⇒ Có 6 cách lấy quả cầu màu trắng ở hộp A và 4 cách lấy quả cầu màu trắng ở hộp B
⇒ n(A.B) = 6.4 = 24.
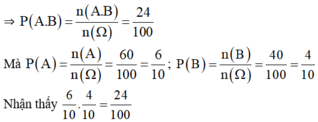
hay P(A.B) = P(A).P(B)
⇒ A và B là biến cố độc lập.
b) Gọi C: “Hai quả cầu lấy ra cùng màu”.
Ta có: A− : “Quả cầu lấy ra từ hộp thứ nhất màu đen”
B− : “ Quả cầu lấy ra từ hộp thứ hai màu đen”
⇒A−.B− : “Cả hai quả cầu lấy ra đều màu đen”
Nhận thấy A.B và A−.B− xung khắc (Vì không thể cùng lúc xảy ra hai trường hợp 2 quả cầu lấy ra cùng trắng và cùng đen)
Và C=(A.B)∪(A−.B−)
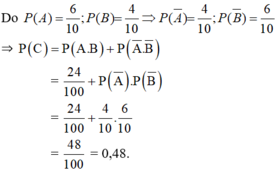
c) C− : “Hai quả cầu lấy ra khác màu”
⇒ P(C− )=1-P(C)=1-0,48=0,52

tham khảo
a) \(A_1\) là biến cố cả 4 quả bóng lấy ra đều có màu xanh; \(P\left(A_1\right)=\dfrac{C^4_5}{C^4_{15}}\)
\(A_2\) là biến cố cả 4 quả bóng lấy ra đều có màu đỏ; \(P\left(A_2\right)=\dfrac{C^4_6}{C^4_{15}}\)
\(A_3\) là biến cố cả 4 quả bóng lấy ra đều có màu vàng; \(P\left(A_3\right)=\dfrac{C^4_4}{C^4_{15}}\)
Khi đó:\(A=A_1\cup A_2\cup A_3\)
Mà \(A_1,A_2,A_3\) là các biến cố xung khắc nên\(P\left(A\right)=P\left(A_1\right)+P\left(A_2\right)+P\left(A_3\right)=\dfrac{1}{65}\)
b) \(B_1\) là biến cố có 2 quả bóng xanh, 1 quả bóng đỏ, 1 quả bóng vàng; \(P\left(B_1\right)=\dfrac{C^2_5.C^1_6.C^1_4}{C^4_{15}}\)
\(B_2\) là biến cố có 1 quả bóng xanh, 2 quả bóng đỏ, 1 quả bóng vàng; \(P\left(B_2\right)=\dfrac{C^1_5.C^2_6.C^1_4}{C^4_{15}}\)
\(B_3\) là biến cố có 1 quả bóng xanh, 1 quả bóng đỏ, 2 quả bóng vàng; \(P\left(B_3\right)=\dfrac{C^1_5.C^1_6.C^2_4}{C^4_{15}}\)
Khi đó:\(B=B_1\cup B_2\cup B_3\)
Mà \(B_1,B_2,B_3\) là các biến cố xung khắc nên
\(P\left(B\right)=P\left(B_1\right)+P\left(B_2\right)+P\left(B_3\right)=\dfrac{48}{91}\)

Chọn ngẫu nhiên từ hộp 3 quả bóng trong tổng số 13 quả bóng có \({C}_{13}^3 = 286\) cách.
\( \Rightarrow n\left( \Omega \right) = 286\)
a) Gọi \(A\) là biến cố “Cả 3 quả bóng lấy ra đều có cùng màu xanh”, \(B\) là biến cố “Cả 3 quả bóng lấy ra đều có cùng màu đỏ”, \(C\) là biến cố “Cả 3 quả bóng lấy ra đều có cùng màu vàng”
Vậy \(A \cup B \cup C\) là biến cố “Cả 3 quả bóng lấy ra đều có cùng màu”
Chọn ngẫu nhiên từ hộp 3 quả bóng trong tổng số 5 quả bóng xanh có \({C}_5^3 = 10\) cách.
\( \Rightarrow n\left( A \right) = 10 \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega\right)}} = \frac{{10}}{{286}} = \frac{5}{{143}}\)
Chọn ngẫu nhiên từ hộp 3 quả bóng trong tổng số 6 quả bóng đỏ có \({C}_6^3 = 20\) cách.
\( \Rightarrow n\left( B \right) = 20 \Rightarrow P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega \right)}} = \frac{{20}}{{286}} = \frac{{10}}{{143}}\)
Chọn ngẫu nhiên từ hộp 3 quả bóng trong tổng số 2 quả bóng vàng có 0 cách.
\( \Rightarrow n\left( C \right) = 0 \Rightarrow P\left( C \right) = 0\)
\( \Rightarrow P\left( {A \cup B \cup C} \right) = P\left( A \right) + P\left( B \right) + P\left( C \right) = \frac{{15}}{{243}}\)
b) Gọi \(D\) là biến cố “Có đúng 2 quả bóng xanh trong 3 quả bóng lấy ra”
Vậy \(A \cup D\) là biến cố “Có ít nhất 2 quả bóng xanh trong 3 quả bóng lấy ra”
Chọn ngẫu nhiên từ hộp 2 quả bóng trong tổng số 5 quả bóng xanh có \({C}_5^2 = 10\) cách.
Chọn ngẫu nhiên từ hộp 1 quả bóng trong tổng số 8 quả bóng đỏ hoặc vàng có \({C}_8^1 = 8\) cách.
\( \Rightarrow n\left( D \right) = 10.8 = 80 \Rightarrow P\left( D \right) = \frac{{n\left( D \right)}}{{n\left( \Omega \right)}} = \frac{{80}}{{286}} = \frac{{40}}{{143}} \Rightarrow P\left( {A \cup D} \right) = P\left( A \right) + P\left( D \right) = \frac{{45}}{{143}}\)

a, Gọi T là biến cố "Trong 4 quả lấy ra có 3 quả cầu trắng".
\(\left|\Omega\right|=C^4_{15}\)
\(\left|\Omega_T\right|=C^3_7.C^1_8\)
\(\Rightarrow P\left(T\right)=\dfrac{\left|\Omega_T\right|}{\left|\Omega\right|}=\dfrac{C^3_7.C^1_8}{C^4_{15}}=\dfrac{8}{39}\)

tham khảo
A là biến cố "Hai quả bóng lấy ra đều có màu xanh", \(P\left(A\right)=\dfrac{C^2_5}{C^2_9}\)
B là biến cố "Hai quả bóng lấy ra đều có màu đỏ", \(P\left(B\right)=\dfrac{C^2_4}{C^2_9}\)
\(A\cup B\) là biến cố "Hai bóng lấy ra có cùng màu". A và B xung khắc nên:
\(P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)=\dfrac{4}{9}\)
\(\Rightarrow C\)

a) Vì số bi trong hộp thứ nhất và hộp thứ hai là độc lập và việc lấy ra số các bi từ hai hộp là độc lập nên hai biến cố A, B là độc lập.
b)
- Trên A:
+ Hai quả lấy ra đều màu đỏ: \(P=\frac{C^2_3}{C^2_5}=\frac{3}{10}\).
+ Hai quả lấy ra cùng màu: \(P=\frac{C^2_3+C^2_2}{C^2_5}=\frac{4}{10}\)
+ Hai quả lấy ra khác màu: \(P=1-\frac{4}{10}=\frac{6}{10}\).
- Trên B:
+ Hai quả lấy ra đều màu đỏ: \(P=\frac{C^2_4}{C^2_{10}}=\frac{2}{15}\).
+ Hai quả lấy ra cùng màu: \(P=\frac{C^2_4+C^2_6}{C^2_{10}}=\frac{7}{15}\)
+ Hai quả lấy ra khác màu: \(P=1-\frac{7}{15}=\frac{8}{15}\).

Không gian mẫu là kết quả việc chọn ngẫu nhiên 4 quả cầu từ hộp 10 quả cầu.
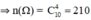
a. A: “ Bốn quả lấy ra cùng màu”
TH1: Bốn quả lấy ra cùng đen
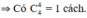
TH2: Bốn quả lấy ra cùng trắng
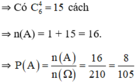
b. B: “ Cả 4 quả lấy ra đều màu đen”
⇒ B−: “ Có ít nhất 1 quả màu trắng”.
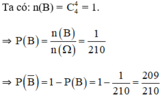

a) \(P\left( A \right) = \frac{6}{{10}} = \frac{3}{5};P\left( B \right) = \frac{7}{8}\)
Không gian mẫu là tập hợp số cách Bạn Long lấy được một quả bóng từ hộp I và Bạn Hải lấy một quả bóng từ hộp II do đó \(n\left( \Omega \right) = 10.8 = 80\)
C: “Bạn Long lấy được quả màu trắng và bạn Hải lấy được quả màu đen”
Công đoạn 1: Bạn Long lấy được quả màu trắng có 6 cách
Công đoạn 2. Bạn Hải lấy được quả màu đen có 7 cách
Theo quy tắc nhân, tập hợp C có 6.7 = 42 (phần tử)
\(P\left( C \right) = P\left( {AB} \right) = \frac{{n\left( C \right)}}{{n\left( \Omega \right)}} = \frac{{42}}{{80}} = \frac{{21}}{{40}}\)
b) \(P\left( A \right).P\left( B \right) = \frac{3}{5}.\frac{7}{8} = \frac{{21}}{{40}}\)
Vậy P(AB) = P(A).P(B).