Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
+ Ta có: ![]()
+ Tại t1 và t2 ngược pha nhau => a1 = - a2 = -80√3 cm/s2
+ Tại cùng 1 thời điểm t1 có:
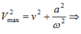
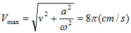

Chọn C
+ Nhận thấy thời điểm t1 vuông pha với thời điểm t2, đồng thời a và v luôn vuông pha nhau.
Sửa dụng công thức độc lập cho a và v tại thời điểm t, và công thức độc lập cho a1 và a2 ở 2 hai thời điểm t và t + 3T/4 ta được:
![]()
![]()

Đáp án A
+ Chọn chiều dương hướng xuống.
+ Thời gian lò xo bị nén là
T
6
, do đó vẽ VTLG ta suy ra được độ dãn ban đầu của lò xo là ![]() do chọn chiều dương hướng xuống nên tại vị trí lò xo không biến dạng
∆
l
0
có li độ x = -
∆
l
0
do chọn chiều dương hướng xuống nên tại vị trí lò xo không biến dạng
∆
l
0
có li độ x = -
∆
l
0
+ Khi vật đến vị trí lò xo không biến dạng thì vật có li độ:
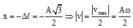
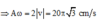
+ Mặt khác: 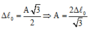
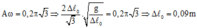
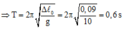

Chọn chiều dương hướng xuống, gốc O tại VTCB. Gọi a là độ dãn của lò xo khi vật cân bằng, li độ của vật khi lò xo dãn ∆ l là ∆ l -a (cm); ω là tần số góc và A là biên độ của vật.
Ta có hệ:
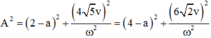
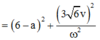
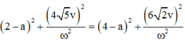
![]()
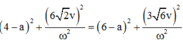
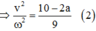
Giải hệ (1) và (2) ta tìm được
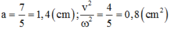
Từ đó tính được A = 8,022 cm.
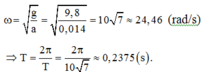
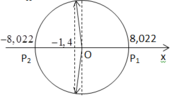
Thời gian lò xo dãn trong một chu kì ứng với vật chuyển động giữa hai li độ -1,4 cm và 8,022cm. Ta chỉ cần tính tốc độ trung bình khi vật đi từ điểm có li độ -1,4 cm đến biên có li độ 8,022 cm với thời gian chuyển động t= T 4 + T 2 π . a r c sin ( a A ) = 0 , 066 ( s )
và quãng đường s = A + a = 9,422 (cm).
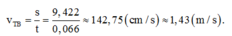



Chọn B
+ |a| ≥ 80 cm/s2 chia VTLG thành 4 phần; 1 phần tương ứng T/6
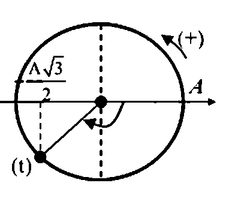
+ Biểu diễn VTLG, từ đó suy ra: