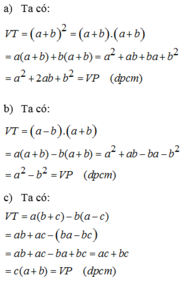Lời giải:

Giả sử $(a^2+b^2, ab)>1$. Khi đó, gọi $p$ là ước nguyên tố lớn nhất của $(a^2+b^2,ab)$

$\Rightarrow a^2+b^2\vdots p; ab\vdots p$

Vì $ab\vdots p\Rightarrow a\vdots p$ hoặc $b\vdots p$

Nếu $a\vdots p$. Kết hợp $a^2+b^2\vdots p\Rightarrow b^2\vdots p$

$\Rightarrow b\vdots p$

$\Rightarrow p=ƯC(a,b)$ . Mà $(a,b)=1$ nên vô lý 

Tương tự nếu $b\vdots p$
Vậy điều giả sử là sai. Tức là $(a^2+b^2, ab)=1$

a, a(b+c)−b(a−c)a(b+c)−b(a−c)

=ab+ac−(ab−bc)=ab+ac−(ab−bc)

=ab+ac−ab+bc=ab+ac−ab+bc

=ac+bc=ac+bc

=(a+b)c=(a+b)c

b,(a+b)(a−b)(a+b)(a−b)

=(aa+ab)−(ab+bb)=(aa+ab)−(ab+bb)

=aa+ab−ab−bb

a) <

b) <

c) >

d) <

a)  18 2 < 10 3

b)  3 2 + 4 2 < ( 3 + 4 ) 2

c)  100 2 + 30 2 < ( 100 + 30 ) 2

d)  a 2 + b 2 > ( a - b ) 2 với a ∈   N * ;   b ∈   N * .  

a) 13 2 = 169 < 216 = 6 3

b)  6 2 + 8 2 = 100 < 196 = ( 6 + 8 ) 2

c)  13 2 - 9 2 = 88 > 16 = ( 13 - 9 ) 2

d)  a 2 + b 2 < a 2 + b 2 + 2 a b = ( a + b ) 2 và với (a Î N*; b Î N*).