
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) xét tg AMB và tg AMC có
MB=MC(gt)
gAMB = gAMC (=90o)
AM chung
=> tg AMB = tgAMC (c-g-c)
=> AB=AC
xét tg ABM và tg ACM có
gAMB = AMC (=90o)
gBAM = g CAM (gt)
AM chung
=> tg ABM = tg ACM (g-c-g)
=> AB=AC (2 cạnh t/ư)

\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)



cái này nhìn hơi khó hiểu các cậu thông cảm nha tại máy đểu quá í mà nên sai kí tự.
cứu mình ạ. Nhanh đc thì tốt!!! CẢM ƠN. Bạn nào mà giúp mình đc thì thi toán sẽ đc điểm tốt nha!! <3


Ta có: \(x^2-\dfrac{1}{4}=0\)
\(x^2=0-\dfrac{1}{4}=-\dfrac{1}{4}\)
Vì x2 ≥ 0 ở mọi x
Mà x2 ≤ 0
Nên đa thức f(x) không có nghiệm
Cho f(x)=0
=>x^2-1/4=0
=>x^2=0+1/4
=>x^2=1/4
=>x=1/2 hoặc x=-1/2
Vậy nghiệm của đa thức trên là 1/2 và -1/2

\(\Leftrightarrow x+\dfrac{2}{3}=\dfrac{6}{7}\\ \Leftrightarrow x=\dfrac{6}{7}-\dfrac{2}{3}=\dfrac{4}{21}\)

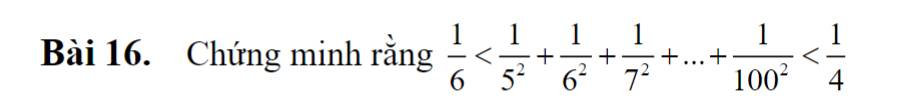 Cứu mình gấp ạ!!! Mình sắp thi rồi!!!
Cứu mình gấp ạ!!! Mình sắp thi rồi!!!

Gọi các phân số cần tìm là: \(\dfrac{a}{b}\) theo bài ra ta có:
\(\dfrac{a}{b}\) = \(\dfrac{a+2}{b\times2}\)
a.(b x 2) = (a + 2) x b
ab x 2 = ab + 2b
ab = 2b
a = 2
Ta có: \(\dfrac{2}{b}\) > \(\dfrac{1}{5}\) = \(\dfrac{2}{10}\)
⇒ b < 10 ⇒ b = 1; 2; 3; 4; 5; 6; 7; 8; 9
Vì \(\dfrac{2}{b}\) không phải là số tự nhiên nên b \(\in\) {3; 4; 5; 6; 7; 8; 9}
Bài 16:
\(\dfrac{1}{6}\) < \(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\) + \(\dfrac{1}{7^2}\) +...+ \(\dfrac{1}{100^2}\) < \(\dfrac{1}{4}\)
\(\dfrac{1}{5^2}\) < \(\dfrac{1}{4.5}\) = \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\)
\(\dfrac{1}{6^2}\) < \(\dfrac{1}{5.6}\) = \(\dfrac{1}{5}\) - \(\dfrac{1}{6}\)
............................
\(\dfrac{1}{100^2}\) < \(\dfrac{1}{99.100}\) = \(\dfrac{1}{99}\) - \(\dfrac{1}{100}\)
Cộng vế với vế ta có:
\(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\)+...+ \(\dfrac{1}{100^2}\) < \(\dfrac{1}{4}\) - \(\dfrac{1}{100}\) < \(\dfrac{1}{4}\) (1)
\(\dfrac{1}{5^2}\) > \(\dfrac{1}{5.6}\) = \(\dfrac{1}{5}\) - \(\dfrac{1}{6}\)
\(\dfrac{1}{6^2}\) > \(\dfrac{1}{6.7}\) = \(\dfrac{1}{6}\) - \(\dfrac{1}{7}\)
...............................
\(\dfrac{1}{100^2}\) > \(\dfrac{1}{100.101}\) = \(\dfrac{1}{100}\) - \(\dfrac{1}{101}\)
Cộng vế với vế ta có:
\(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\) + ... + \(\dfrac{1}{100^2}\) > \(\dfrac{1}{5}\) - \(\dfrac{1}{101}\)= \(\dfrac{96}{505}\) > \(\dfrac{96}{576}\) = \(\dfrac{1}{6}\) (2)
Kết hợp (1) và (2) ta có:
\(\dfrac{1}{6}\) < \(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\) +...+ \(\dfrac{1}{100^2}\) < \(\dfrac{1}{4}\) (đpcm)