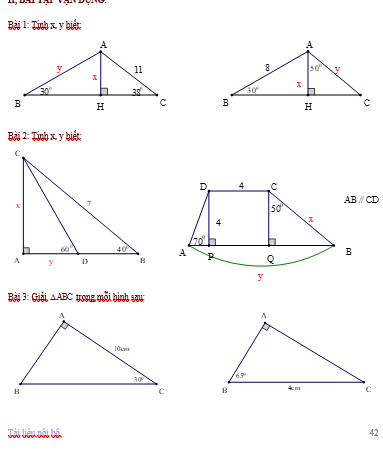
Bài 3: 

a: Ta có: ΔABC vuông tại A

nên \(\widehat{B}+\widehat{C}=90^0\)

hay \(\widehat{B}=60^0\)

Xét ΔABC vuông tại A có 

\(AB=AC\cdot\tan30^0\)

\(=\dfrac{10\sqrt{3}}{3}\left(cm\right)\)

Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(AB^2+AC^2=BC^2\)

\(\Leftrightarrow BC=\dfrac{20\sqrt{3}}{3}\left(cm\right)\)

1/

Để hàm số trên đồng biến 

Thì m-1 > 0 ⇔ m>1

2/

a,<bạn tự vẽ>

b,Theo phương trình hoành độ giao điểm

\(2x=-x+3\Leftrightarrow3x=3\Leftrightarrow x=1\)

Thay x=1 vào y=2x

y=2.1=2

Vậy tọa độ giao điểm A là (1;2)

3/ Để (d) đi qua điểm M (1;-2)

Thì x=1 và y=-2

Thay x=1 và y=-2 vào (d)

\(-2=a\cdot1+1\Leftrightarrow a=-3\)

vậy ....

Bài 1:

Để hàm số bậc nhất \(y=\left(m-1\right)x+3\) đồng biến.

=> \(m-1>0.\)

<=> \(m>1.\)

Bài 2:

b) Xét phương trình hoành độ giao điểm của 2 hàm số trên ta có:

       \(\text{2x = -x + 3.}\)

<=> \(\text{2x + x - 3= 0.}\)

<=> \(\text{3x - 3 = 0.}\)

<=> \(x=1.\)

=>   \(y=2.\)

Vậy A(1; 2).

Bài 3:

Vì (d) đi qua điểm M(1; -2).

=> -2 = a. 1 + 1.

<=> a = -3.

Vậy a = -3. 

Bài 1: 

a: ĐKXĐ: \(x\ge\dfrac{3}{2}\)

Bài 4:

\(a,A=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}}\\ P=A:B=\dfrac{\sqrt{x}+1}{\sqrt{x}}\cdot\dfrac{x-1}{\sqrt{x}+1}=\dfrac{x-1}{\sqrt{x}}\\ b,P\sqrt{x}=m-\sqrt{x}+x\\ \Leftrightarrow x-1=m-\sqrt{x}+x\\ \Leftrightarrow m=\sqrt{x}-1\)

Câu 16: A

Câu 14: C

Câu 12: A

\(A=\sqrt{3-\sqrt{5}}-\sqrt{4-\sqrt{15}}+\sqrt{6-3\sqrt{3}}\)

\(=\dfrac{1}{\sqrt{2}}\cdot\left(\sqrt{6-2\sqrt{5}}-\sqrt{8-2\sqrt{15}}+\sqrt{12-6\sqrt{3}}\right)\)

\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{5}-1-\sqrt{5}+\sqrt{3}+3-\sqrt{3}\right)\)

=2/căn 2=căn 2

\(B=\sqrt{4-\sqrt{7}}-\sqrt{14-5\sqrt{3}}-\sqrt{5+\sqrt{21}}\)

\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{8-2\sqrt{7}}-\sqrt{28-10\sqrt{3}}-\sqrt{10+2\sqrt{21}}\right)\)

\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{7}-1-5+\sqrt{3}-\sqrt{7}-\sqrt{3}\right)\)

=-6/căn 2=-3căn2

\(C=\sqrt{11-6\sqrt{2}}-\sqrt{6-4\sqrt{2}}+\sqrt{7-2\sqrt{6}}\)

=3-căn 2-2+căn 2+căn 6-1

=căn 6

\(D=\sqrt{6-\sqrt{11}}-\sqrt{10+3\sqrt{11}}+2\sqrt{2}-1\)

\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{12-2\sqrt{11}}-\sqrt{20+6\sqrt{11}}\right)+2\sqrt{2}-1\)

\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{11}-1-\sqrt{11}-3\right)+2\sqrt{2}-1\)

=-1

\(F=\sqrt{6+3\sqrt{3}}-\sqrt{2+\sqrt{3}}+\sqrt{6-4\sqrt{2}}\)

\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{12+6\sqrt{3}}-\sqrt{4+2\sqrt{3}}\right)+2-\sqrt{2}\)

=1/căn 2(3+căn 3-căn 3-1)+2-căn 2

=căn 2+2-căn 2

=2

a: Xét (O) có

ΔAMB nội tiếp

AB là đường kính

Do đó: ΔAMB vuông tại M

=>\(\widehat{AMB}=90^0\)

b: Xét ΔOMC vuông tại M có MH là đường cao

nên \(HC\cdot HO=HM^2\left(1\right)\)

Xét ΔMAB vuông tại M có MH là đường cao

nên \(HA\cdot HB=HM^2\left(2\right)\)

Từ (1) và (2) suy ra \(HC\cdot HO=HA\cdot HB\)

c: Xét tứ giác AMBQ có

O là trung điểm của AB và MQ

Do đó: AMBQ là hình bình hành

Hình bình hành AMBQ có AB=MQ

nên AMBQ là hình bình hành

Bài 1: 

a: Xét tứ giác NPIK có 

\(\widehat{NKP}=\widehat{NIP}\left(=90^0\right)\)

Do đó: NPIK là tứ giác nội tiếp

hay N,P,I,K cùng thuộc 1 đường tròn

b: Xét tứ giác MKHI có

\(\widehat{MKH}+\widehat{MIH}=180^0\)

Do đó: MKHI là tứ giác nội tiếp

hay M,K,H,I cùng thuộc 1 đường tròn