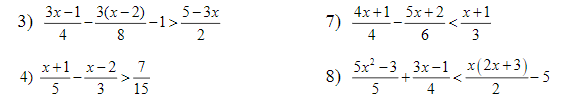Bạn cần câu nào?

câu nào cx đc ạ càng nhiều càng tốt

ê, tưng câu 1 thôi

đăng từng câu 1 thôi

Xét ΔADC và ΔBCD có 

CD chung

AD=BC(ABCD là hình thang cân)

AC=BD(ABCD là hình thang cân)

Do đó: ΔADC=ΔBCD(c-c-c)

Suy ra: \(\widehat{ACD}=\widehat{BDC}\)(hai góc tương ứng)

hay \(\widehat{IDC}=\widehat{ICD}\)

Xét ΔIDC có \(\widehat{IDC}=\widehat{ICD}\)(cmt)

nên ΔIDC cân tại I(Định lí đảo của tam giác cân)

Ta có: \(\widehat{IAB}=\widehat{ICD}\)(hai góc so le trong, AB//CD)

\(\widehat{IBA}=\widehat{IDC}\)(hai góc so le trong, AB//CD)

mà \(\widehat{ICD}=\widehat{IDC}\)(cmt)

nên \(\widehat{IAB}=\widehat{IBA}\)

Xét ΔIAB có \(\widehat{IAB}=\widehat{IBA}\)(cmt)

nên ΔIAB cân tại I(Định lí đảo của tam giác cân)

chẳng nhìn rõ cái gì bạn ạ 

\(P=\left(x^2+4xy+4y^2\right)+\left(y^2+8y+16\right)+16\\ P=\left(x+2y\right)^2+\left(y+4\right)^2+16\ge16\\ P_{min}=16\Leftrightarrow\left\{{}\begin{matrix}x=-2y=8\\y=-4\end{matrix}\right.\)

thanh kìu :))))))))

a: Xét tứ giác AMBN có

I là trung điểm của AB

I là trung điểm của MN

Do đó: AMBN là hình bình hành

phần b và c nữa bn

\(\Leftrightarrow6x^2-9x-32x+48=0\)

\(\Leftrightarrow3x\left(2x-3\right)-16\left(2x-3\right)=0\)

\(\Leftrightarrow\left(2x-3\right)\left(3x-16\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{16}{3}\end{matrix}\right.\)

\(x\) = 1,5; \(x\) = \(\dfrac{16}{3}\)

1: \(=\left(y-1\right)^2\)

2: \(=\left(x+1+5\right)\left(x+1-5\right)=\left(x+6\right)\left(x-4\right)\)

3: =(1-2x)(1+2x)

\(=\left(2-3x\right)\left(4+6x+9x^2\right)\)

5: \(=\left(x+3\right)^3\)

6: \(=\left(2x-y\right)^3\)

cảm ơn vị cứu tinh