
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{9x+9}-2\sqrt{\dfrac{x+1}{4}}=4\left(đk:x\ge-1\right)\)
\(\Leftrightarrow3\sqrt{x+1}-\sqrt{x+1}=4\)
\(\Leftrightarrow2\sqrt{x+1}=4\)
\(\Leftrightarrow\sqrt{x+1}=2\Leftrightarrow x+1=4\Leftrightarrow x=3\left(tm\right)\)

Câu 61:
a: \(B=\dfrac{3}{\sqrt{x}-2}+\dfrac{4}{\sqrt{x}+2}-\dfrac{12}{x-4}\)
\(=\dfrac{3}{\sqrt{x}-2}+\dfrac{4}{\sqrt{x}+2}-\dfrac{12}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3\left(\sqrt{x}+2\right)+4\left(\sqrt{x}-2\right)-12}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3\sqrt{x}+6+4\sqrt{x}-8-12}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{7\sqrt{x}-14}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{7\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{7}{\sqrt{x}+2}\)
b: \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{\sqrt{x}-1}{\sqrt{x}+1}+\dfrac{3\sqrt{x}+1}{1-x}\)
\(=\dfrac{\left(\sqrt{x}+1\right)}{\sqrt{x}-1}+\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2+\left(\sqrt{x}-1\right)^2-3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}+1-3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2x-3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(2\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\)
Câu 60
Khi a=2 thì hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}\left(2^2-1\right)x+y=3\\2x-y=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x+y=3\\2x-y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x=10\\2x-y=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=2x-7=2\cdot2-7=-3\end{matrix}\right.\)

a)\(đkx\ge1,x\ne-1\)
\(\sqrt{\dfrac{x-1}{x+1}}=2\)
\(\Leftrightarrow\dfrac{x-1}{x+1}=4\)
\(\Leftrightarrow x-1=4x-4\)
\(\Leftrightarrow x=1\)(nhận)
Vậy S=\(\left\{1\right\}\)
c)đk\(25x^2-10x+1=\) \(\left(5x-1\right)^2\ge0\Leftrightarrow x\ge\dfrac{1}{5}\)
\(\sqrt{25x^2-10x+1}+2x=1\)
\(\Leftrightarrow\sqrt{\left(5x-1\right)^2}+2x=1\)
\(\Leftrightarrow5x-1+2x=1\)
\(\Leftrightarrow x=\dfrac{2}{7}\)(nhận)
Vậy S=\(\left\{\dfrac{2}{7}\right\}\)
c: Ta có: \(\sqrt{25x^2-10x+1}+2x=1\)
\(\Leftrightarrow\left|5x-1\right|=1-2x\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-1=1-2x\left(x\ge\dfrac{1}{5}\right)\\5x-1=2x-1\left(x< \dfrac{1}{5}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{7}\left(nhận\right)\\x=0\left(nhận\right)\end{matrix}\right.\)

a: góc AMB=1/2*180=90 độ
góc AMN+góc AKN=180 độ
=>AMNK là tứ giác nội tiếp
b: ΔCAB vuông tại A có AM vuông góc CB
nên CA^2=MC*CB

bài 7
A=\(\dfrac{x+2}{\sqrt{x^3}-1}+\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\left(x+\sqrt{x}+1\right)}+\dfrac{-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
A=\(\dfrac{x+2+x-1-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
A=\(\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)=\(\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+x+1\right)}\)
A=\(\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
bài 8
P=\(\left[\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)^2}\right].\dfrac{\left(x-1\right)^2}{4x}\)
P=\(\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2\left(\sqrt{x}+1\right)}.\dfrac{\left(x-1\right)^2}{4x}\)
P=\(\dfrac{2\sqrt{x}}{\left(x-1\right)\left(\sqrt{x}-1\right)}.\dfrac{\left(x-1\right)^2}{4x}\)=\(\dfrac{x-1}{2\sqrt{x}\left(\sqrt{x}-1\right)}\)
P=\(\dfrac{\sqrt{x}+1}{2\sqrt{x}}\)
bài 9
P=\(\left[\dfrac{2\sqrt{xy}}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}-\dfrac{\sqrt{x}+\sqrt{y}}{2\left(\sqrt{x}-\sqrt{y}\right)}\right].\dfrac{2\sqrt{x}}{\sqrt{x}-\sqrt{y}}\)
P=\(\dfrac{4\sqrt{xy}-\left(\sqrt{x}+\sqrt{y}\right)^2}{2\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}.\dfrac{2\sqrt{x}}{\sqrt{x}-\sqrt{y}}\)
P=\(\dfrac{2\sqrt{xy}-x-y}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}.\dfrac{\sqrt{x}}{\sqrt{x}-\sqrt{y}}\)
P=\(\dfrac{-\left(\sqrt{x}-\sqrt{y}\right)^2}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}.\dfrac{\sqrt{x}}{\sqrt{x}-\sqrt{y}}\)
P=\(\dfrac{-\sqrt{x}}{\sqrt{x}+\sqrt{y}}\)
bài 10
P=\(\left[\dfrac{1}{\sqrt{x}+2}-\dfrac{2}{\left(\sqrt{x}+2\right)^2}\right]:\left[\dfrac{2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\dfrac{1}{\sqrt{x}-2}\right]\)
P=\(\dfrac{\sqrt{x}+2-2}{\left(\sqrt{x}+2\right)^2}:\dfrac{2-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
P=\(\dfrac{\sqrt{x}}{\left(\sqrt{x}+2\right)^2}.\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{-\sqrt{x}}\)=\(\dfrac{-\left(\sqrt{x}-2\right)}{\sqrt{x}+2}\)





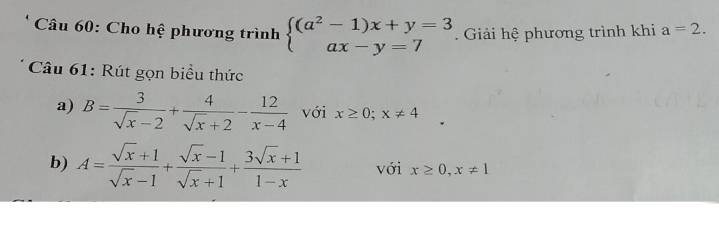

 vẽ hình vs làm câu a) . b) thôi ạ, e cần gấp lắm á
vẽ hình vs làm câu a) . b) thôi ạ, e cần gấp lắm á



Bài 2:
e) \(\sqrt{4x-8}-12\sqrt{\dfrac{x-2}{9}}=\sqrt{x-2}-12\left(đk:x\ge2\right)\)
\(\Leftrightarrow\sqrt{4}.\sqrt{x-2}-12.\sqrt{\dfrac{1}{9}}.\sqrt{x-2}=\sqrt{x-2}-12\)
\(\Leftrightarrow2\sqrt{x-2}-4\sqrt{x-2}=\sqrt{x-2}-12\)
\(\Leftrightarrow3\sqrt{x-2}=12\)
\(\Leftrightarrow\sqrt{x-2}=4\)
\(\Leftrightarrow x-2=16\Leftrightarrow x=18\left(tm\right)\)
Cảm ơn bạn