
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


6:
=y^2+y+1/4-1/4
=(y+1/2)^2-1/4>=-1/4
Dấu = xảy ra khi y=-1/2
7:
=5(x^2+4/5x-3/5)
=5(x^2+2*x*2/5+4/25-19/25)
=5(x+2/5)^2-19/5>=-19/5
Dấu = xảy ra khi x=-2/5
8: =7(x^2-12/7x-6/7)
=7(x^2-2*x*6/7+36/49-78/49)
=7*(x-6/7)^2-78/7>=-78/7
Dấu = xảy ra khi x=6/7
9: =x^2-2x+1+y^2-4y+4
=(x-1)^2+(y-2)^2>=0
Dấu = xảy ra khi x=1 và y=2
10: =x^2-x+1/4+1/4
=(x-1/2)^2+1/4>=1/4
Dấu = xảy ra khi x=1/2

6:
=y^2+y+1/4-1/4
=(y+1/2)^2-1/4>=-1/4
Dấu = xảy ra khi y=-1/2
7:
=5(x^2+4/5x-3/5)
=5(x^2+2*x*2/5+4/25-19/25)
=5(x+2/5)^2-19/5>=-19/5
Dấu = xảy ra khi x=-2/5
8: =7(x^2-12/7x-6/7)
=7(x^2-2*x*6/7+36/49-78/49)
=7*(x-6/7)^2-78/7>=-78/7
Dấu = xảy ra khi x=6/7
9: =x^2-2x+1+y^2-4y+4
=(x-1)^2+(y-2)^2>=0
Dấu = xảy ra khi x=1 và y=2
10: =x^2-x+1/4+1/4
=(x-1/2)^2+1/4>=1/4
Dấu = xảy ra khi x=1/2

Bài 1:
\(N=2x^2+4y^2-2x-4y+15=2\left(x^2-x+\dfrac{1}{4}\right)+\left(4y^2-4y+1\right)+\dfrac{27}{2}=2\left(x-\dfrac{1}{2}\right)^2+\left(2y-1\right)^2+\dfrac{27}{2}\ge\dfrac{27}{2}\)
\(minN=\dfrac{27}{2}\Leftrightarrow x=y=\dfrac{1}{2}\)
Bài 2:
\(\Leftrightarrow4x^2+12x+9-25x^2+50x-25=0\)
\(\Leftrightarrow21x^2-62x+16=0\)
\(\Leftrightarrow\left(3x-8\right)\left(7x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{8}{3}\\x=\dfrac{2}{7}\end{matrix}\right.\)

làm bừa thui,ai tích mình mình tích lại
Số số hạng là :
Có số cặp là :
50 : 2 = 25 ( cặp )
Mỗi cặp có giá trị là :
99 - 97 = 2
Tổng dãy trên là :
25 x 2 = 50
Đáp số : 50
A = |x-7| + |x-5| = |7-x| + |x-5| ≥ |7-x + x-5| = 2
minA = 2
đạt khi 7-x và x-5 cùng dấu <=> (7-x)(x-5) ≥ 0 <=> 5 ≤ x ≤ 7
B = (2x-1)² - 3|2x-1| + 2 = |2x-1|² - 2.|2x-1|.(3/2) + 9/4 + 2 - 9/4
B = (|2x-1| - 3/2)² - 1/4 ≥ -1/4
minB = -1/4
đạt khi: |2x-1| = 3/2 <=> 2x-1 = 3/2 hoặc 2x-1 = -3/2 <=> x = 5/4 hoặc x = -1/4
C = |x² + x + 1| + |x² + x -12| = |x² + x + 1| + |12 - x² - x | ≥
≥ |x² + x + 1 + 12 - x² - x| = |13| = 13
minC = 13
đạt khi (x² + x +1) và (12 - x² - x) cùng dấu
<=> (x²+x+1)(12-x²-x) ≥ 0 <=> -1 ≤ x²+x ≤ 12 <=>
{x² + x + 1 ≥ 0
{x² + x -12 ≤ 0
<=>
(x + 4)(x - 3) ≤ 0 <=> -4 ≤ x ≤ 3
tóm lại:
minC = 13 đạt khi -4 ≤ x ≤ 3
học tốt

Bài 1: Tìm x: (2x-6)^3 + (5-x)^3 + (1-x)^3 = 0
Bài 2: Tìm GTNN :
A= x^2 -2x -4
B= x^2 -x +5
C= 4x^2 +2x -9
D= 2x^2 -4x +7
Giúp tớ với, tớ đang cần gấp

1.
$x(x+2)(x+4)(x+6)+8$
$=x(x+6)(x+2)(x+4)+8=(x^2+6x)(x^2+6x+8)+8$
$=a(a+8)+8$ (đặt $x^2+6x=a$)
$=a^2+8a+8=(a+4)^2-8=(x^2+6x+4)^2-8\geq -8$
Vậy $A_{\min}=-8$ khi $x^2+6x+4=0\Leftrightarrow x=-3\pm \sqrt{5}$
2.
$B=5+(1-x)(x+2)(x+3)(x+6)=5-(x-1)(x+6)(x+2)(x+3)$
$=5-(x^2+5x-6)(x^2+5x+6)$
$=5-[(x^2+5x)^2-6^2]$
$=41-(x^2+5x)^2\leq 41$
Vậy $B_{\max}=41$. Giá trị này đạt tại $x^2+5x=0\Leftrightarrow x=0$ hoặc $x=-5$

Giải như sau.
(1)+(2)⇔x2−2x+1+√x2−2x+5=y2+√y2+4⇔(x2−2x+5)+√x2−2x+5=y2+4+√y2+4⇔√y2+4=√x2−2x+5⇒x=3y(1)+(2)⇔x2−2x+1+x2−2x+5=y2+y2+4⇔(x2−2x+5)+x2−2x+5=y2+4+y2+4⇔y2+4=x2−2x+5⇒x=3y
⇔√y2+4=√x2−2x+5⇔y2+4=x2−2x+5, chỗ này do hàm số f(x)=t2+tf(x)=t2+t đồng biến ∀t≥0∀t≥0
Công việc còn lại là của bạn !
\(\left(x+6\right)\left(2x+1\right)=0\)
<=> \(\orbr{\begin{cases}x+6=0\\2x+1=0\end{cases}}\)
<=> \(\orbr{\begin{cases}x=-6\\x=-\frac{1}{2}\end{cases}}\)
Vậy....
hk tốt
^^
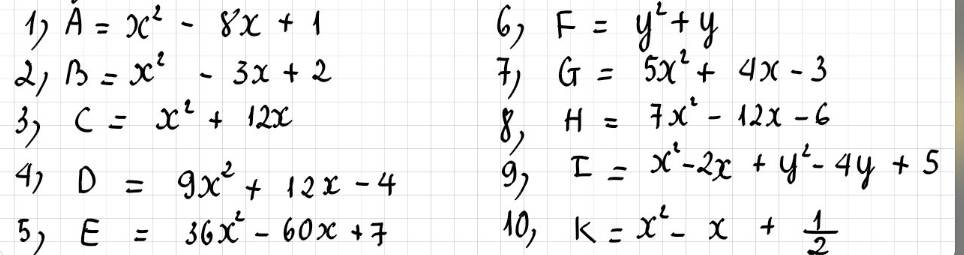
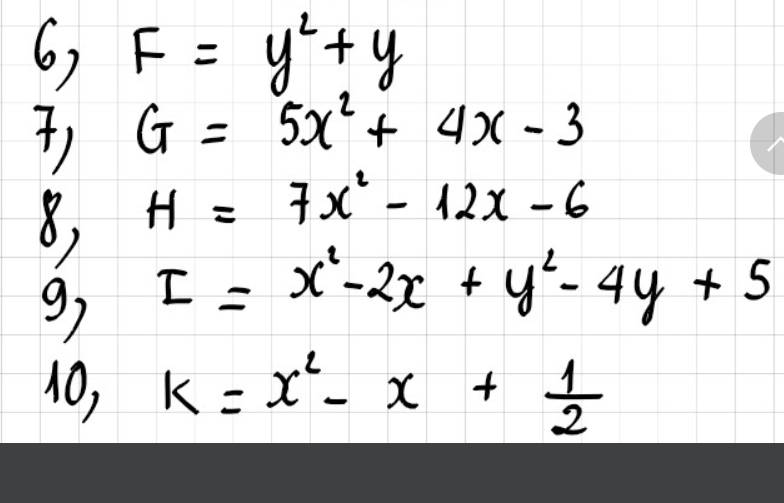
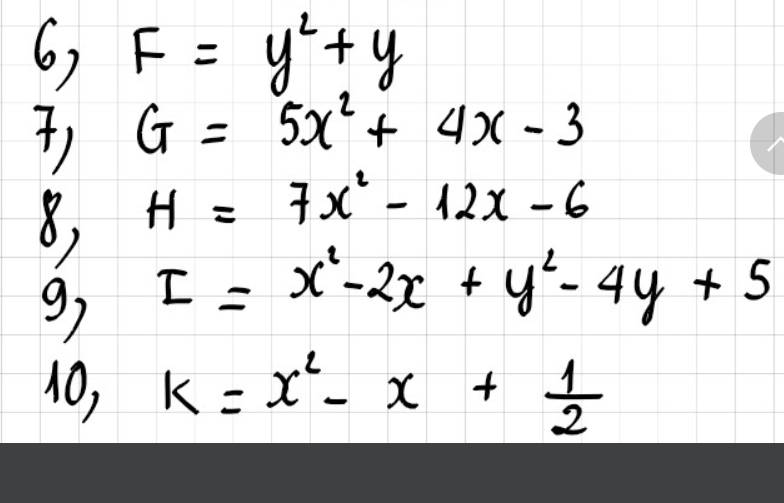
1
\(A=x^2-8x+1=x^2-2.4x+16-15\\ =\left(x-4\right)^2-15\ge-15\)
Min A \(=-15\) khi \(x=4\)
2
\(B=x^2-3x+2=x^2-2.\dfrac{3}{2}+\dfrac{9}{4}-\dfrac{1}{4}\\ =\left(x-\dfrac{3}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\)
Min B \(=-\dfrac{1}{4}\) khi \(x=\dfrac{3}{2}\)
3
\(C=x^2+12x=x^2+2.6x+6^2-36\\=\left(x+6\right)^2-36\ge-36\)
Min C \(=-36\) khi `x=-6`
4
\(D=9x^2+12x-4\\ =\left(3x\right)^2+2.3x.2+2^2-8\\ =\left(3x-2\right)^2-8\ge-8\)
Min D \(=-8\) khi \(x=\dfrac{2}{3}\)
5
\(E=36x^2-60x+7=\left(6x\right)^2-2.6x.5+5^2-18\\ =\left(6x-5\right)^2-18\ge-18\)
Min E \(=-18\) khi \(x=\dfrac{5}{6}\)
6:
=y^2+y+1/4-1/4
=(y+1/2)^2-1/4>=-1/4
Dấu = xảy ra khi y=-1/2
7:
=5(x^2+4/5x-3/5)
=5(x^2+2*x*2/5+4/25-19/25)
=5(x+2/5)^2-19/5>=-19/5
Dấu = xảy ra khi x=-2/5
8: =7(x^2-12/7x-6/7)
=7(x^2-2*x*6/7+36/49-78/49)
=7*(x-6/7)^2-78/7>=-78/7
Dấu = xảy ra khi x=6/7
9: =x^2-2x+1+y^2-4y+4
=(x-1)^2+(y-2)^2>=0
Dấu = xảy ra khi x=1 và y=2
10: =x^2-x+1/4+1/4
=(x-1/2)^2+1/4>=1/4
Dấu = xảy ra khi x=1/2