Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
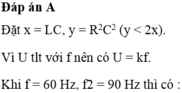
I 1 = U 1 Z 1 = k f Z 1 I 2 = U 2 Z 2 = k f 2 Z 2 ⇔ k f Z 1 = 2 k f 2 Z 2 ⇔ R 2 + Z L 1 - Z C 1 2 ω 1 2 = R 2 + Z L 2 - Z C 2 2 4 ω 2 2 I 1 = 2 I 2
⇔ R 2 C 2 ω 1 2 + ω 1 2 L C - 1 2 ω 1 4 C 2 = R 2 C 2 ω 2 2 + ω 2 2 L C - 1 2 4 ω 2 4 C 2 ⇔ 20 ٫ 25 ω 1 2 y + ω 1 2 x - 1 2 = ω 2 2 y + ω 2 2 x - 1 2 1
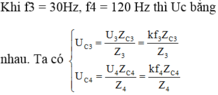
Suy ra U C 3 = U C 4 ⇔ Z 3 = Z 4 ⇔ Z L 3 - Z C 3 2 = Z L 4 - Z C 4 2 ⇔ Z L 3 - Z C 3 = Z C 4 - Z L 4
⇒ φ R C = - π 4 ⇒ R = Z C = 1 ω C ⇒ ω = 1 R C = 1 y ⇒ f 1 = 1 2 π y = 204 H z
Đáp án C
- Hai giá trị 
cho cùng I
Đây là phương trình bậc hai theo 
, theo định lí Vi-et, ta có:
- Hai giá trị 
cho cùng
Đây là phương trình bậc hai theo 
, theo định lí Vi-et, ta có:
Thay (2) vào (1) ta được
- Khi 
thì URC lệch
135
0
so với
U
L
. Từ giản đồ vecto, ta có:
Thay vào (3) ta được:
Đáp án A
Có
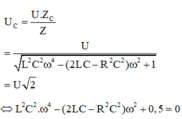
Đây là dạng tam thức bậc 2. Áp dụng định lý Viete
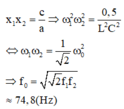
+ Khi f = f 1 = 50 H z
thì u c vuông pha với u => u cùng pha với
+ Khi f 2 = 30 H z và f 3 = 40 H z thì u c cho cùng một giá trị nên:
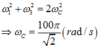
Ta có:
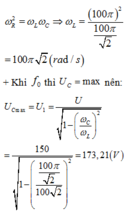
=> Chọn A.
Đáp án A
+ Áp dụng kết quả bài toán chuẩn hóa ω biến thiên thể U R L max
→ U A N max có nghĩa là U R L max với n = 1 2 + 1 4 + 1 2 R 2 L C , kết hợp với
11 L = 50 C R 2 → n = 1 , 1
+Với n = f R L 2 f R 2 ⇒ f R = f R L 2 = 30 11 1 , 1 = 30 10 H z .
→ n - 1 2 2 = f R 2 f R C 2 - 1 2 2 = f R 2 f 1 2 - 1 2 2 f R 2 f 2 2 - 1 2 2 → f 1 = 100 H z .
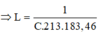
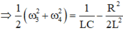
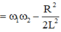
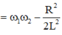
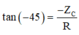
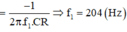
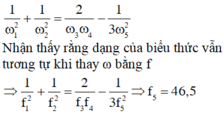
+ ta có:
+ Ta có:
+ Ta có:
=> Chọn C.