Câu hỏi của Phạm Thùy Dung - Toán lớp 7 - Học toán với OnlineMath

Câu hỏi của Phạm Thùy Dung - Toán lớp 7 - Học toán với OnlineMath

a) Ta có góc DAC=60^o+góc BAC= góc BAE

Xét tam giác DAC và tam giác BAE có:

DA=BA

góc DAC=góc BAC

AC=AE

Nên tam giác ADC= tam giác ABE (c.g.c)

b) J thuộc DC sao cho DJ=BI

Xét tam giác ADJ và tam giác ABI có:

AD=AB

góc ADJ=góc ABI (vì tam giác ADC= tam giác ABE)

DJ=BI

Nên tam giác ADJ= tam giác ABI (c.g.c)

Suy ra AJ=AI (2 cạnh tương ứng)

Mà góc JAI= góc JAB+ góc BAI = góc JAB+ góc DAJ=60^o

Nên tam giác AIJ đều nên góc =60^o

Lại có tam giác ADJ= tam giác ABI: 

Nên góc AIB=góc AJD=180^o - góc AJI=120^o

=> góc BID = góc AIB- góc AID =60^o

c, Théo câu a ta có BE=CD do đó DM=BN

Lại có tam giác DAC = tam giác BAE nên góc ABN= góc ADM

Xét tam giác ABN và tam giác ADM có:

AB=AD

góc ABN= góc ADM

BN=DM

=> tam giác ABN = tam giác ADM => AN=AM; góc DAM= góc BAN 

=> góc DAM - góc BAM = góc BAN- góc BAM = AM=AN; góc MAN= góc DAB =60^o

=> tam giác AMN  là tam giác đều

d, Ta có: 

góc AIE= 180^o - góc AIB =180^o - góc AID - góc BID =180⁰-60⁰-60⁰

= 60^o = AID

=> đpcm

a, ta có : góc DAB=EAC=60độ

=> DAB+BAC=EAC+BAC => DAC=BAE

Cạnh DA=AB và AE=AC 

=> tam giác ADC=ABE ( c.g.c )

a,Xét ΔABEΔABE và ΔADCΔADC có :

AB = AD ( ΔABDΔABD đều )

góc BAE = góc DAC ( góc BAC + 60 độ )

AE = AC ( ΔACEΔACE đều )

⇒⇒ ΔABEΔABE = ΔADCΔADC ( c.g.c )

Vậy ΔABEΔABE = ΔADCΔADC ( c.g.c )

b, Ta có: ^ AEM + ^MEC = 60 độ

mà ^AEM = ACD (Tam giác ABE = tam giác ADC)

=>^MEC + ^MCA = 60 độ

Ta lại có: ^ACE = 60 độ

=>^MCA + ^ACE+ ^MEC = 120 độ

mà ^MCA + ^ACE = ^MCE

=> ^MCE + ^MEC = 120 độ

Ta lại có: ^EMC + ^MCE + ^CEM = 180 độ

mà ^MCE + ^CEM =120 độ (cm trên)

=>^EMC + 120 độ =180 độ

=> ^EMC = 180 độ - 120 độ =60 độ

Ta lại có: ^BMC + ^EMC = 180 độ

mà ^EMC = 60 độ

=> ^BMC + 60 độ =180 độ

=> ^BMC = 180 độ - 60 độ = 120 độ (đpcm)

a,Xét ΔABE và ΔADC có :

AB = AD ( ΔABD đều )

góc BAE = góc DAC ( góc BAC + 60 độ )

AE = AC ( ΔACE đều )

⇒ ΔABE = ΔADC ( c.g.c )

Vậy ΔABE = ΔADC ( c.g.c )

tự kẻ hình :

a, xét tam giác DAC và BAE có : 

AD = AB do tam giác ABD đều (gt)

AC = AE do tam giác ACE đều (gt)

góc DAB + góc BAC = góc DAC 

góc BAC + góc  CAE = góc BAE

góc DAB = góc CAE = 60 do ...

=> góc DAC = góc BAE 

=> tam giác DAC = tam giác BAE (c - g - c)

ai lam ý b đi tui cũng ko bet làm

cho tam giác ABC có 3 góc nhọn, (AB<AC) . vẽ về phía ngoài tam giác ABC  các tam giác đều ABD;ACE .gọi I là giao điểm của CD và BE ; K là giao điểm của AB và DC. 

a) CMR:  tam giác ADC= tam giác ABE

b) chứng minh : góc DIB= 60 độ 

c) gọi M và N lần lượt là trung điểm CD và DE .CMR :  tam giác AMN đều 

d) CMR : IA là tia phân giác của góc DIE 

thằng ngu kia sao lại chép lại đề bài

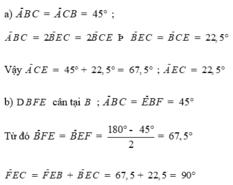
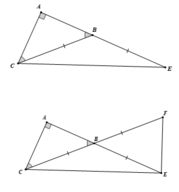
 HIH ĐÓ BN

tam giác đều ACE kiểu gì thế