Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
Do đó: ΔABD=ΔACD

a) Xét tam giác vuông ABM và tam giác vuông NCA có:
NC=AB( gt)
CA=BM ( gt)
=> Tam giác ABM = Tam giác NCA
b) Xét tam giác vuông NCA và tam giác vuông BAC có:
AC chung
NC=BA
=> Tam giác NCA =Tam giác BAC
=> ^NAC =^BCA
mà hai góc trên ở vị trí so le trong
=> NA//BC (1)
c) Xét tam giác vuông ABC và tam giác vuông BMA có:
AB chung
AC=BM
=> Tam giác vuông ABC = Tam giác vuông BMA
=> ^MAB=^ABC
mà hai góc trên ở vị trí so le trong
=> MA//CB (2)
từ (1) , (2) => N, A, M thẳng hàng
Ta lại có: NA=AM ( Tam giác ABM =tam giác NCA)
=> A là trung điểm MN

Do tam giác ABC cân tại A nên AB = AC, từ đó tam giác ABD = tam giác ACD (cạnh huyền - cạnh góc vuông).
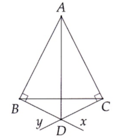

a) Xét Δ ABD vuông tại B và Δ ACD vuông tại C có:
+ AD chung.
+ AB = AC (Tam giác ABC cân tại A).
\(\Rightarrow\Delta ABD=\Delta ACD\) (cạnh huyền - cạnh góc vuông).
b) \(\Delta ABD=\Delta ACD\left(cmt\right).\Rightarrow\) \(\widehat{BDA}=\widehat{CDA}\) (2 góc tương ưng).
\(\Rightarrow\) DA là tia phân giác của \(\widehat{BDC}.\)