Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`Answer:`
a) Phân tích \(\frac{7x}{15x-5}\) được xác định khi: \(15x-5\ne0\Rightarrow15x\ne5\Rightarrow x\ne\frac{1}{3}\)
b) \(\frac{x+4}{x^2-9}=\frac{x+4}{\left(x-3\right)\left(x+3\right)}\)
Vậy điều kiện xác định: `x\ne+-3`
c) Vì phân thức có chứa ẩn dưới mẫu nên để cho phân thức xác định thì:
\(36x^2-25\ne0\Rightarrow36x^2\ne25\Rightarrow x^2\ne\frac{25}{36}\Rightarrow x\ne\pm\frac{5}{6}\)
d) Phân thức xác định khi \(x^2+2x+3\ne0\Rightarrow\left(x+1\right)^2+2\ne0\)
Nhận thấy \(\left(x+1\right)^2+2\ge2>0\forall x\)
\(\Rightarrow\left(x+1\right)^2+2\ne0\) (Luôn đúng)
Vậy phân thức trên được xác định với mọi `x`

1.a)\(\frac{x^3}{x^2-4}-\frac{x}{x-2}-\frac{2}{x+2}\)
\(=\frac{x^3}{\left(x+2\right)\left(x-2\right)}-\frac{x}{x-2}-\frac{2}{x+2}\)
Để biểu thức được xác định thì:\(\left(x+2\right)\left(x-2\right)\ne0\)\(\Rightarrow x\ne\pm2\)
\(\left(x+2\right)\ne0\Rightarrow x\ne-2\)
\(\left(x-2\right)\ne0\Rightarrow x\ne2\)
Vậy để biểu thức xác định thì : \(x\ne\pm2\)
b) để C=0 thì ....
1, c , bn Nguyễn Hữu Triết chưa lm xong
ta có : \(/x-5/=2\)
\(\Rightarrow\orbr{\begin{cases}x-5=2\\x-5=-2\end{cases}}\Rightarrow\orbr{\begin{cases}x=7\\x=3\end{cases}}\)
thay x = 7 vào biểu thứcC
\(\Rightarrow C=\frac{4.7^2\left(2-7\right)}{\left(7-3\right)\left(2+7\right)}=\frac{-988}{36}=\frac{-247}{9}\)KL :>...
thay x = 3 vào C
\(\Rightarrow C=\frac{4.3^2\left(2-3\right)}{\left(3-3\right)\left(3+7\right)}\)
=> ko tìm đc giá trị C tại x = 3

a, ĐỂ \(\frac{3x+3}{x^2-1}=\frac{3x+3}{\left(x+1\right)\left(x-1\right)}\) Xác định
\(\Rightarrow\left(x+1\right)\left(x-1\right)\ne0\)
\(\Rightarrow\hept{\begin{cases}x+1\ne0\\x-1\ne0\end{cases}\Rightarrow\hept{\begin{cases}x\ne-1\\x\ne1\end{cases}}}\)
KL : \(x\ne\pm1\)
b ,
\(\frac{3x+3}{x^2-1}\)xác định
\(\Leftrightarrow x^2-1\ne0\Leftrightarrow x\ne\pm1\)
Vậy điều kiện xác định của \(\frac{3x+3}{x^2-1}\)là \(x\ne\pm1\)
\(\frac{3x+3}{x^2-1}=-2\)
\(\Leftrightarrow\frac{3\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=-2\)
\(\Leftrightarrow\frac{3}{x-1}=-2\)
\(\Leftrightarrow3=-2\left(x-1\right)\)
\(\Leftrightarrow\frac{-3}{2}=x-1\)
\(\Leftrightarrow x=\frac{-1}{2}\)
Vậy \(x=\frac{-1}{2}\)là giá trị cần tìm

\(\frac{x^2+2x}{2x+10}+\frac{x-5}{x}+\frac{50-5x}{2x\left(x+5\right)}=\frac{x^2+2x}{2\left(x+5\right)}+\frac{x-5}{x}+\frac{50-5x}{2x\left(x+5\right)}=\)
\(=\frac{x\left(x^2+2x\right)+2\left(x+5\right)\left(x-5\right)+50-5x}{2x\left(x+5\right)}=\frac{x^3+2x^2+2x^2-50+50-5x}{2x\left(x+5\right)}=\frac{x^3+4x^2-5x}{2x\left(x+5\right)}=\)
\(=\frac{x\left(x^2+4x-5\right)}{2x\left(x+5\right)}=\frac{x\left(x^2+4x-5\right)}{2x\left(x+5\right)}=\frac{x\left(x^2-1+4\left(x-1\right)\right)}{2x\left(x+5\right)}=\frac{x\left(x-1\right)\left(x+5\right)}{2x\left(x+5\right)}\)
a/ Để biểu thức xác đinh => 2x(x+5) khác 0 => x khác 0 và x khác -5
b/ Gọi biểu thức là A. Rút gọn A ta được:
\(A=\frac{x\left(x-1\right)\left(x+5\right)}{2x\left(x+5\right)}=\frac{x-1}{2}\left(x\ne0;x\ne-5\right)\)
A=1 => x-1=2 => x=3
c/ A=-1/2 <=> x-1=-1 => x=0
d/ A=-3 <=> x-1=-6 => x=-5

a. ĐK \(\hept{\begin{cases}x\ne0\\x+5\ne0\end{cases}\Rightarrow\hept{\begin{cases}x\ne0\\x\ne-5\end{cases}}}\)
b. \(A=\frac{x^2+2x}{2x\left(x+5\right)}+\frac{x-5}{x}+\frac{50-5x}{2x\left(x+5\right)}=\frac{x\left(x^2+2x\right)+2\left(x-5\right)\left(x+5\right)+50-5x}{2x\left(x+5\right)}\)
\(=\frac{x^3+2x^2+2x^2-50+50-5x}{2x\left(x+5\right)}=\frac{x^3+4x^2-5x}{2x\left(x+5\right)}\)
\(=\frac{x\left(x+5\right)\left(x-1\right)}{2x\left(x+5\right)}=\frac{x-1}{2}\)
Để \(A=1\Rightarrow\frac{x-1}{2}=1\Rightarrow x=3\)
Để \(A=-3\Rightarrow\frac{x-1}{2}=-3\Rightarrow x=-5\)
Vậy với x=3 thì A=1 ; với x=-5 thì A=-3

Bài 1:
a) x≠2
Bài 2:
a) x≠0;x≠5
b) x2−10x+25x2−5x=(x−5)2x(x−5)=x−5x
c) Để phân thức có giá trị nguyên thì x−5x phải có giá trị nguyên.
=> x=−5
Bài 3:
a) (x+12x−2+3x2−1−x+32x+2)⋅(4x2−45)
=(x+12(x−1)+3(x−1)(x+1)−x+32(x+1))⋅2(2x2−2)5
=(x+1)2+6−(x−1)(x+3)2(x−1)(x+1)⋅2⋅2(x2−1)5
=(x+1)2+6−(x2+3x−x−3)(x−1)(x+1)⋅2(x−1)(x+1)5
=[(x+1)2+6−(x2+2x−3)]⋅25
=[(x+1)2+6−x2−2x+3]⋅25
=[(x+1)2+9−x2−2x]⋅25
=2(x+1)25+185−25x2−45x
=2(x2+2x+1)5+185−25x2−45x
=2x2+4x+25+185−25x2−45x
=2x2+4x+2+185−25x2−45x
=2x2+4x+205−25x2−45x
c) tự làm, đkxđ: x≠1;x≠−1
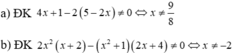

a, đkxđ : \(4x+6\ne0\Leftrightarrow x\ne-\frac{3}{2}\)
b, đkxđ : \(\left(x-1\right)\left(x+1\right)\ne0\Leftrightarrow x\ne-1;1\)
c, đkxđ : \(36x^2-25\ne0\Leftrightarrow\left(6x-5\right)\left(6x+5\right)\ne0\Leftrightarrow x\ne-\frac{5}{6};-\frac{5}{6}\)
d, đkxđ : \(x^2+2x+3=x^2+2x+1+2=\left(x+1\right)^2+2>0\rightarrow x\in R\)