tham khảo:

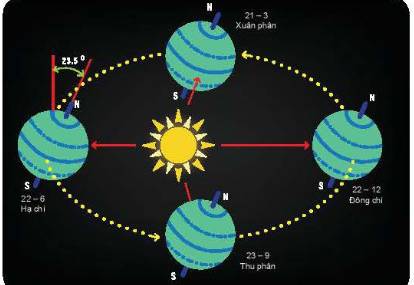
a) Vì trục quay của Trái Đất luôn cố định hướng về một phương cố định trong không gian, và mặt phẳng quỹ đạo cũng không thay đổi trong quá trình quay quanh Mặt Trời.

b) Trong quá trình chuyển động quanh Mặt Trời, hình chiếu của trục Trái Đất trên mặt phẳng quỹ đạo sẽ thay đổi theo thời gian và tạo thành một đường tròn có bán kính bằng góc nghiêng của trục quay so với mặt phẳng quỹ đạo. Khi Trái Đất ở vị trí xa nhất (khoảng 4/7 quỹ đạo) và gần nhất (khoảng 3/7 quỹ đạo) so với Mặt Trời, thì hình chiếu của trục quay của Trái Đất trên mặt phẳng quỹ đạo sẽ nằm trên đường thẳng nối tâm Trái Đất và Mặt Trời.

a) Chiều dài một vòng của quỹ đạo là : \(9000.2.\pi \) (km)

Quãng đường vệ tinh đã chuyển động được sau 1 giờ là \(\frac{{9000.2.\pi }}{3} = 6000\pi \)(km)

Quãng đường vệ tinh đã chuyển động được sau 3 giờ là \(18000\pi \)(km)

Quãng đường vệ tinh đã chuyển động được sau 5 giờ là \(\frac{{9000.2.\pi }}{3}.5 = 30000\pi \)(km)

b)Vệ tinh chuyển động được quãng đường 200 000 km sau sô giờ là : \(\frac{{200000}}{{6000\pi }} \approx 11\)(giờ)

a)

\(\begin{array}{l}F = 0\;\\ \Rightarrow \frac{1}{2}\left( {1 - \cos \alpha } \right) = 0\;\; \Leftrightarrow 1 - \cos \alpha  = 0\;\; \Leftrightarrow \cos \alpha  = 1\; \Leftrightarrow \alpha  = k2\pi \;\left( {k \in \mathbb{Z}} \right)\end{array}\)

b) \(F = 0,25\; \Rightarrow \frac{1}{2}\left( {1 - \cos \alpha } \right) = 0,25\; \Leftrightarrow 1 - \cos \alpha  = \frac{1}{2}\;\; \Leftrightarrow \cos \alpha  = \frac{1}{2}\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\alpha  = \frac{\pi }{3} + k2\pi }\\{\alpha  =  - \frac{\pi }{3} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\)

c) \(F = 0,5\;\; \Rightarrow \frac{1}{2}\left( {1 - \cos \alpha } \right) = 0,5\; \Leftrightarrow 1 - \cos \alpha  = 1\; \Leftrightarrow \cos \alpha  = 0\; \Leftrightarrow \alpha  = \frac{\pi }{2} + k\pi \;\;\left( {k \in \mathbb{Z}} \right)\)

d) \(F = 1\; \Leftrightarrow \frac{1}{2}\left( {1 - \cos \alpha } \right) = 1\;\; \Leftrightarrow 1 - \cos \alpha  = 2\; \Leftrightarrow \cos \alpha  =  - 1\; \Leftrightarrow \alpha  = \pi  + k2\pi \;\left( {k \in \mathbb{Z}} \right)\)

Sau một phút di chuyển, van V đã quay được một góc lượng giác có số đo góc là: \(\alpha=11\cdot60=660\left(rad\right)\)

Khi đó tọa độ điểm V biểu diễn cho góc lượng giác trên có tọa độ là: \(V\left(58\cdot cos\alpha,58\cdot sin\alpha\right)\approx\left(56;15,2\right)\)

Từ đó, khoảng cách từ van đến mặt đất khoảng \(58-15,2\approx42,8\left(cm\right)\)

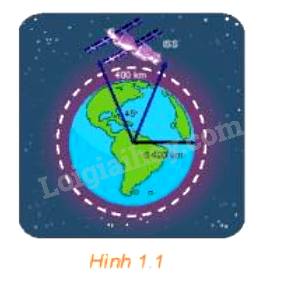
Bán kính quỹ đạo của trạm vũ trụ quốc tế là R = 6 400 + 400 = 6 800 (km).

Đổi \(45{}^\circ =45\cdot \frac{\pi }{180}=\frac{\pi }{4}\).

Vậy trong khi được trạm mặt đất theo dõi, trạm ISS đã di chuyển một quãng đường có độ dài là \(l = R\alpha \text{ = }6\,800\cdot \frac{\pi }{4}\approx 5\,340,708\approx 5\,341\,(km)\).

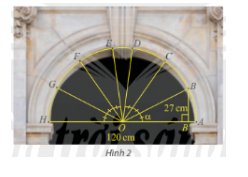
Ta có: \(OA = OB = 120:2 = 60\)

Xét tam giác OBB’ có:

\(\sin \widehat {BOB'} = \frac{{BB'}}{{OB}} = \frac{{27}}{{60}} = \frac{9}{{20}}\)

\(\widehat {AOC} = 2\widehat {BOB'}\)

(Vì số đo cung AC gấp 2 lần số đo cung AB)

Xét tam giác OCC’ vuông tại C’ có:

\(\begin{array}{l}\sin \widehat {COC'} = \frac{{CC'}}{{OC}}\\ \Leftrightarrow CC' = OC.\sin \widehat {COC'} = OC.\sin \left( {2\widehat {BOB'}} \right)\end{array}\)

Mà \(\sin \left( {2\widehat {BOB'}} \right) = 2.\sin \widehat {BOB'}.cos\widehat {BOB'}\)

\( = 2.\frac{9}{{20}}.\frac{{\sqrt {319} }}{{20}} = \frac{{9\sqrt {319} }}{{400}}\)

Vậy khoảng cách từ C đến AH là \(60.\frac{{9\sqrt {319} }}{{200}} \approx 48,2cm\).

a, Ta có: \(\left\{{}\begin{matrix}AB\perp SA\left(do:SA\perp\left(ABCD\right)\right)\\AB\perp AD\left(gt\right)\end{matrix}\right.\)

\(\Rightarrow AB\perp\left(SAD\right)\)

Từ C kẻ CH // AB  ⇒ CH ⊥ (SAD)

⇒ d (C, (SAD)) = CH = 2a

b, Ta có: \(\left(SAC\right)\cap\left(ABCD\right)=AC\)

Hạ DE ⊥ AC ⇒ DE ⊥ (SAC)

⇒ d(D, (SAC)) = DE

Ta có: AC = 2a√2, AH = HC 2a và HD = a

Xét tam giác HDC vuông tại H, có: \(DC=\sqrt{HD^2+HC^2}=a\sqrt{5}\)

Xét tam giác AHC vuông cân tại H, có: \(\widehat{HAC}=45^o=\widehat{DAE}\)

Xét tam giác ADE vuông tại E, có: \(DE=AD.sin\widehat{DAE}=\dfrac{3a\sqrt{2}}{2}\)