
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a
= { 1*( 1+1/2+1/3+1/4) } / { 1 * ( 1-1/2 +1/3-1/4)} : { 3*(1+1/2+1/3+1/4)} / { 2*( 1-1/2 +1/3-1/4)}
Sau đó bn tự tính ra nhé cứ tính nhu bình thường sẽ ra.
Mà mình thấy máy câu này yêu cầu tính chứ có bảo tính theo cách hợp lí đâu? Vì thế bn cứ lấy máy tính tính như bình thường là được .

a) \(2.04:\left(-3.12\right)=\dfrac{204}{-312}=\dfrac{-17}{26}\)
b) \(\left(-1\dfrac{1}{2}\right):1.25=\dfrac{-3}{2}:\dfrac{5}{4}=\dfrac{-3}{2}\cdot\dfrac{4}{5}=\dfrac{-12}{10}=\dfrac{-6}{5}\)
c) \(4:5\dfrac{3}{4}=4:\dfrac{23}{4}=4\cdot\dfrac{4}{23}=\dfrac{16}{23}\)
d) \(10\dfrac{3}{7}:5\dfrac{3}{14}=\dfrac{73}{7}:\dfrac{73}{14}=\dfrac{2}{1}\)

a, -4\(\dfrac{3}{5}\).2\(\dfrac{4}{3}\) < \(x\) < -2\(\dfrac{3}{5}\): 1\(\dfrac{6}{15}\)
- \(\dfrac{23}{5}\).\(\dfrac{10}{3}\) < \(x\) < - \(\dfrac{13}{5}\): \(\dfrac{21}{15}\)
- \(\dfrac{46}{3}\) < \(x\) < - \(\dfrac{13}{7}\)
\(x\) \(\in\) {-15; -14;-13;..; -2}
a) Ta có \(-4\dfrac{3}{5}\cdot2\dfrac{4}{3}=-\dfrac{23}{5}\cdot\dfrac{10}{3}=-\dfrac{46}{3}\) và \(-2\dfrac{3}{5}\div1\dfrac{6}{15}=-\dfrac{13}{5}\div\dfrac{7}{5}=-\dfrac{13}{7}\)
Do đó \(-\dfrac{46}{3}< x< -\dfrac{13}{7}\)
Lại có \(-\dfrac{46}{3}\le-15\) và \(-\dfrac{13}{7}\ge-2\)
Suy ra \(-15\le x\le-2\), x ϵ Z
b) Ta có \(-4\dfrac{1}{3}\left(\dfrac{1}{2}-\dfrac{1}{6}\right)=-\dfrac{13}{3}\cdot\dfrac{1}{3}=-\dfrac{13}{9}\) và \(-\dfrac{2}{3}\left(\dfrac{1}{3}-\dfrac{1}{2}-\dfrac{3}{4}\right)=-\dfrac{2}{3}\cdot\dfrac{-11}{12}=\dfrac{11}{18}\)
Do đó \(-\dfrac{13}{9}< x< \dfrac{11}{18}\)
Lại có \(-\dfrac{13}{9}\le-1\) và \(\dfrac{11}{18}\ge0\)
Suy ra \(-1\le x\le0\), x ϵ Z

2:
\(B=\left(\dfrac{1}{2^2}-1\right)\left(\dfrac{1}{3^2}-1\right)\cdot...\cdot\left(\dfrac{1}{100^2}-1\right)\)
\(=\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{2}+1\right)\left(\dfrac{1}{3}-1\right)\left(\dfrac{1}{3}+1\right)\cdot...\cdot\left(\dfrac{1}{100}-1\right)\left(\dfrac{1}{100}+1\right)\)
\(=\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{3}-1\right)\cdot...\cdot\left(\dfrac{1}{100}-1\right)\left(\dfrac{1}{2}+1\right)\left(\dfrac{1}{3}+1\right)\cdot...\cdot\left(\dfrac{1}{100}+1\right)\)
\(=\dfrac{-1}{2}\cdot\dfrac{-2}{3}\cdot...\cdot\dfrac{-99}{100}\cdot\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{101}{100}\)
\(=-\dfrac{1}{100}\cdot\dfrac{101}{2}=\dfrac{-101}{200}< -\dfrac{100}{200}=-\dfrac{1}{2}\)

Cậu ơi, câu đầu tớ vẫn chưa hiểu ý câu hỏi là như nào hết, cậu có thể viết lại cho tớ đko ạ? 
Câu 1 là : \(\dfrac{-2}{5}:1\dfrac{1}{3}-\left(\dfrac{1}{2}\right)^2\)

a) \(\dfrac{-5}{9}.\dfrac{3}{11}+\dfrac{-13}{18}.\dfrac{3}{11}\)
\(=\dfrac{3}{11}.\left(\dfrac{-5}{9}+\dfrac{-13}{9}\right)\)
\(=\dfrac{3}{11}.\left(-2\right)\)
\(=\dfrac{-6}{11}\)
b) \(\dfrac{11}{2}.2\dfrac{1}{3}-1\dfrac{1}{5}.1\dfrac{1}{2}\)
\(=\dfrac{11}{3}.\dfrac{7}{3}-\dfrac{6}{5}.\dfrac{3}{2}\)
\(=\dfrac{77}{9}-\dfrac{9}{5}\)
\(=\dfrac{385}{45}-\dfrac{81}{45}\)
\(=\dfrac{304}{45}\)
c) \(1\dfrac{1}{9}.\dfrac{2}{145}-4\dfrac{1}{3}-\dfrac{2}{145}+\dfrac{2}{145}\)
\(=\dfrac{10}{9}.\dfrac{2}{145}-\dfrac{8}{3}\)
\(=\dfrac{4}{261}-\dfrac{8}{3}\)
\(=\dfrac{4}{261}-\dfrac{696}{261}\)
\(=-\dfrac{692}{261}\)
d) \(1-\dfrac{1}{2}+2-\dfrac{2}{3}+3-\dfrac{3}{4}+4-\dfrac{1}{4}-3-\dfrac{1}{3}-2-\dfrac{1}{2}-1\)
\(=\left(1-1\right)+\left(2-2\right)+\left(3-3\right)+4-\left(\dfrac{1}{2}+\dfrac{1}{2}\right)-\left(\dfrac{2}{3}+\dfrac{1}{3}\right)-\left(\dfrac{3}{4}+\dfrac{1}{4}\right)\)
\(=0+0+0+4-1-1-1\)
\(=4-3\)
\(=1\)

a, Ta có :\(A=\dfrac{1}{2^1}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{49}}+\dfrac{1}{2^{50}}\\ \Rightarrow2A=1+\dfrac{1}{2^1}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{49}}\\ \Rightarrow2A-A=\left(1+\dfrac{1}{2^1}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{49}}\right)-\left(\dfrac{1}{2^1}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{50}}\right)\\ \Rightarrow A=1-\dfrac{1}{2^{50}}< 1\\ \Rightarrow A< 1\) Vậy \(A< 1\)
b, Ta có :
\(B=\dfrac{1}{3^1}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{100}}\\ \Rightarrow3B=1+\dfrac{1}{3^1}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{99}}\\ \Rightarrow3B-B=\left(1+\dfrac{1}{3^1}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{99}}\right)-\left(\dfrac{1}{3^1}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{100}}\right)\\ \Rightarrow2B=1-\dfrac{1}{3^{100}}< 1\\ \Rightarrow B< \dfrac{1}{2}\)Vậy \(B< \dfrac{1}{2}\)
c, Ta có :
\(C=\dfrac{1}{4^1}+\dfrac{1}{4^2}+...+\dfrac{1}{4^{1000}}\\ \Rightarrow4C=1+\dfrac{1}{4^1}+\dfrac{1}{4^2}+...+\dfrac{1}{4^{999}}\\\Rightarrow4C-C=\left(1+\dfrac{1}{4^1}+\dfrac{1}{4^2}+...+\dfrac{1}{4^{999}}\right)-\left(\dfrac{1}{4^1}+\dfrac{1}{4^2}+...+\dfrac{1}{4^{1000}}\right)\\ \Rightarrow3C=1-\dfrac{1}{4^{1000}}< 1\\ \Rightarrow C< \dfrac{1}{3}\)Vậy \(C< \dfrac{1}{3}\)
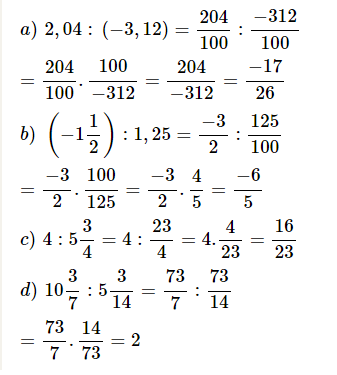
A = \(\dfrac{1}{1+2+3}\) + \(\dfrac{1}{1+2+3+4}\) +......+\(\dfrac{1}{1+2+3+4+....+59}\)
A = \(\dfrac{1}{(3+1).3:2}\) + \(\dfrac{1}{(4+1).4:2}\)+......+\(\dfrac{1}{(59+1).59:2}\)
A = \(\dfrac{2}{3.4}\) + \(\dfrac{2}{4.5}\) +.....+ \(\dfrac{2}{59.60}\)
A = 2.(\(\dfrac{1}{3.4}+\dfrac{1}{4.5}+....+\dfrac{1}{59.60}\))
A = 2. ( \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) +....+ \(\dfrac{1}{59}\) - \(\dfrac{1}{60}\))
A = 2. ( \(\dfrac{1}{3}\) - \(\dfrac{1}{60}\))
A = 2. \(\dfrac{19}{60}\)
A = \(\dfrac{19}{30}\)