1.

\(-4\le\dfrac{x^2-2x-7}{x^2+1}\le1\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2-2x-7\le x^2+1\\-4x^2-4\le x^2-2x-7\end{matrix}\right.\) (Do \(x^2+1>0\))

\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-4\\\left[{}\begin{matrix}x\ge1\\x\le-\dfrac{3}{5}\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x\ge1\\-4\le x\le-\dfrac{3}{5}\end{matrix}\right.\)

2.

\(\dfrac{1}{13}\le\dfrac{x^2-2x-2}{x^2-5x+7}\le1\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2-5x+7\le13x^2-26x-26\\x^2-2x-2\le x^2-5x+7\end{matrix}\right.\) (Do \(x^2-5x+7>0\))

\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\ge\dfrac{11}{4}\\x\le-1\end{matrix}\right.\\x\le3\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{11}{4}\le x\le3\\x\le-1\end{matrix}\right.\)

Giải từng bất phương trình bằng cách chuyển vế rồi lập bảng xét dấu là ra nha bạn

Yêu cầu gì bạn

a: =>\(\dfrac{x^2+2x-13-x+1}{x-1}< 0\)

=>\(\dfrac{x^2+x-12}{x-1}< 0\)

=>\(\dfrac{\left(x+4\right)\left(x-3\right)}{x-1}< 0\)

=>1<x<3 hoặc x<-4

b: =>\(\dfrac{3x^2+4x-3x-4}{x-1}< 3\)

=>3x+4<3

=>3x<-1

=>x<-1/3

c: TH1: 2x^2-3x+1>0 và x+2>0

=>(2x-1)(x-1)>0 và x+2>0

=>x>1

TH2: (2x-1)(x-1)<0 và x+2<0

=>x<-2 và 1/2<x<1

=>Loại

a, \(\left|3x+1\right|>2\)

\(\Leftrightarrow\left(\left|3x+1\right|\right)^2>4\)

\(\Leftrightarrow9x^2+6x+1>4\)

\(\Leftrightarrow9x^2+6x-3>0\)

\(\Leftrightarrow3\left(3x-1\right)\left(x+1\right)>0\)

\(\Leftrightarrow\left[{}\begin{matrix}x>\dfrac{1}{3}\\x< -1\end{matrix}\right.\)

b, \(\left|2x-1\right|\le1\)

\(\Leftrightarrow\left(\left|2x-1\right|\right)^2\le1\)

\(\Leftrightarrow4x^2-4x+1\le1\)

\(\Leftrightarrow4x\left(x-1\right)\le0\)

\(\Leftrightarrow0\le x\le1\)

c, ĐK: \(x\ne13\)

\(\left|\dfrac{2}{x-13}\right|>\dfrac{8}{9}\)

\(\Leftrightarrow\dfrac{1}{\left|x-13\right|}>\dfrac{4}{9}\)

\(\Leftrightarrow4\left|x-13\right|< 9\)

\(\Leftrightarrow16\left(x^2-26x+169\right)< 81\)

\(\Leftrightarrow16x^2-416x+2623< 0\)

\(\Leftrightarrow\dfrac{43}{4}< x< \dfrac{61}{4}\)

\(\Rightarrow\) Có hai giả trị thỏa mãn yêu cầu bài toán

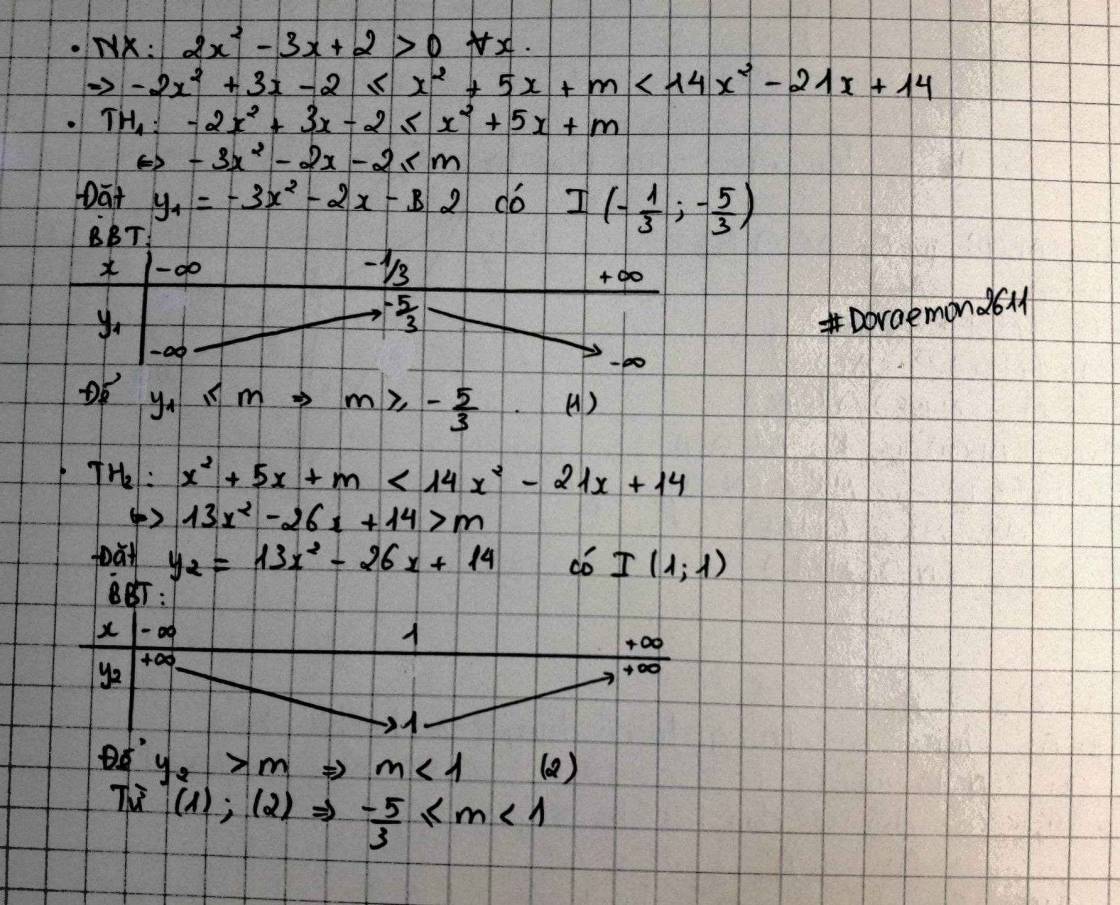
Đk: \(x\in R\)

Có \(2x^2-3x+2>0;\forall x\)

\(-1\le\dfrac{x^2+5x+m}{2x^2-3x+2}< 7\) với \(\forall x\)\(\Leftrightarrow-2x^2+3x-2\le x^2+5x+m< 14x^2-21x+14\) với mọi x

\(\Leftrightarrow\left\{{}\begin{matrix}3x^2+2x+m+2\ge0;\forall x\left(1\right)\\13x^2-26x+14-m>0;\forall x\left(2\right)\end{matrix}\right.\)

Từ \(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}a=3>0\left(lđ\right)\\\Delta\le0\end{matrix}\right.\)\(\Leftrightarrow4-4.3\left(m+2\right)\le0\)\(\Leftrightarrow-20-12m\le0\)\(\Leftrightarrow m\ge\dfrac{-5}{3}\)

Từ \(\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}a=13>0\left(lđ\right)\\\Delta< 0\end{matrix}\right.\)\(\Leftrightarrow m< 1\)

Vậy \(-\dfrac{5}{3}\le m< 1\)

1.

ĐK: \(x\ne7;x\ne-1;x\ne3\)

\(\dfrac{2x-5}{x^2-6x-7}\le\dfrac{1}{x-3}\left(1\right)\)

TH1: \(x< -1\)

\(\left(1\right)\Leftrightarrow\left(2x-5\right)\left(x-3\right)\ge x^2-6x-7\)

\(\Leftrightarrow2x^2-11x+15\ge x^2-6x-7\)

\(\Leftrightarrow x^2-5x+22\ge0\)

\(\Leftrightarrow\) Bất phương trình đúng với mọi \(x< -1\)

TH2: \(-1< x< 3\)

\(\left(1\right)\Leftrightarrow\left(3-x\right)\left(2x-5\right)\ge\left(7-x\right)\left(x+1\right)\)

\(\Leftrightarrow-2x^2+11x-15\ge-x^2+6x+7\)

\(\Leftrightarrow-x^2+5x-22\ge0\)

\(\Rightarrow\) vô nghiệm

TH3: \(3< x< 7\)

Khi đó \(\dfrac{2x-5}{x^2-6x-7}\le0\); \(\dfrac{1}{x-3}>0\)

\(\Rightarrow\) Bất phương trình đúng với mọi \(3< x< 7\)

TH4: \(x>7\)

\(\left(1\right)\Leftrightarrow\left(2x-5\right)\left(x-3\right)\le x^2-6x-7\)

\(\Leftrightarrow2x^2-11x+15\le x^2-6x-7\)

\(\Leftrightarrow x^2-5x+22\le0\)

\(\Rightarrow\) vô nghiệm

Vậy ...

Các bài kia tương tự, chứ giải ra mệt lắm.

Bạn lưu ý:

\(x^2-5x+7=\left(x-\frac{5}{2}\right)^2+\frac{3}{4}>0\) \(\forall x\) nên ta có quyền nhân chéo mà BPT ko ảnh hưởng

Do đó BPT tương đương:

\(\frac{1}{13}\left(x^2-5x+7\right)\le x^2-2x-2\le x^2-5x+7\)

\(\Leftrightarrow\left\{{}\begin{matrix}\frac{1}{13}\left(x^2-5x+7\right)\le x^2-2x-2\\x^2-2x-2\le x^2-5x+7\end{matrix}\right.\)

Bạn giải 2 BPT này ra (rất đơn giản) rồi lấy giao hai miền nghiệm là được

BPT 1: \(\Leftrightarrow x^2-5x+7\le13x^2-26x-26\)

\(\Leftrightarrow12x^2-21x-33\ge0\)

\(\Rightarrow\left[{}\begin{matrix}x\le-1\\x\ge\frac{11}{4}\end{matrix}\right.\)

BPT 2 \(\Leftrightarrow3x\le9\Leftrightarrow x\le3\)

Kết hợp lại ta được: \(\left[{}\begin{matrix}x\le-1\\\frac{11}{4}\le x\le3\end{matrix}\right.\)