Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a) Ta thấy:
$6^2+4,5^2=7,5^2\Leftrightarrow AB^2+AC^2=BC^2$
Theo định lý Pitago đảo ta suy ra $ABC$ là tam giác vuông tại $A$
b)
$S_{ABC}=\frac{AB.AC}{2}=\frac{AH.BC}{2}$
$\Rightarrow AH=\frac{AB.AC}{BC}=\frac{6.4,5}{7,5}=3,6$ (cm)
$\sin B=\frac{AC}{BC}=\frac{4,5}{7,5}\Rightarrow \widehat{B}\approx 36,8^0$
$\Rightarrow \widehat{C}\approx 90^0-36,78^0=53,2^0$

a: Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>ABOC là tứ giác nội tiếp
=>A,B,C,O cùng thuộc một đường tròn
b: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2\)
mà OB=OD
nên \(OD^2=OH\cdot OA\)
=>\(\dfrac{OD}{OH}=\dfrac{OA}{OD}\)
Xét ΔODA và ΔOHD có
\(\dfrac{OD}{OH}=\dfrac{OA}{OD}\)
\(\widehat{DOA}\) chung
Do đó: ΔODA đồng dạng với ΔOHD

1: \(AO=\sqrt{3^2+8^2}=\sqrt{73}\left(cm\right)\)
BC=2*R=6cm
\(CA=\sqrt{AB^2+BC^2}=\sqrt{8^2+6^2}=10\left(cm\right)\)
BD=6*8/10=4,8cm
2: Xét ΔBCE có
O là trung điểm của BC
OH//CE
=>H là trung điểm của BE
ΔOBE cân tại O
mà OH là trung tuyến
nên OH là phân giác của góc BOE
Xét ΔOBA và ΔOEA có
OB=OE
góc BOA=góc EOA
OA chung
=>ΔOBA=ΔOEA
=>góc OEA=90 độ
=>AE là tiếp tuyến của (O)

a: Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc một đường tròn
b: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC và AO là phân giác của góc BAC
Ta có: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
từ (1) và (2) suy ra AO là đường trung trực của BC
=>OA\(\perp\)BC
c: Xét ΔOBA vuông tại B có \(sinBAO=\dfrac{OB}{OA}=\dfrac{1}{2}\)
nên \(\widehat{BAO}=30^0\)
Ta có: AO là phân giác của góc BAC
=>\(\widehat{BAC}=2\cdot\widehat{BAO}=60^0\)
Ta có: ΔOBA vuông tại B
=>\(BO^2+BA^2=OA^2\)
=>\(BA^2=\left(2R\right)^2-R^2=3R^2\)
=>\(BA=R\sqrt{3}\)
Xét ΔBAC có AB=AC và \(\widehat{BAC}=60^0\)
nên ΔBAC đều
=>\(S_{BAC}=\dfrac{BA^2\cdot\sqrt{3}}{4}=\dfrac{3R^2\cdot\sqrt{3}}{4}\)

1: Xét (O) có
AB là tiếp tuyến có B là tiếp điểm
AC là tiếp tuyến có C là tiếp điểm
Do đó: AB=AC
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(1)
Ta có: AB=AC
nên A nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
hay OA\(\perp\)BC tại H
Áp dụng hệ thức lượng trong tam giác vuông vào ΔOBA vuông tại B có BH là đường cao ứng với cạnh huyền OA, ta được:
\(BO^2=OH\cdot OA\)
\(\Leftrightarrow OH=\dfrac{3^2}{6}=1.5\left(cm\right)\)

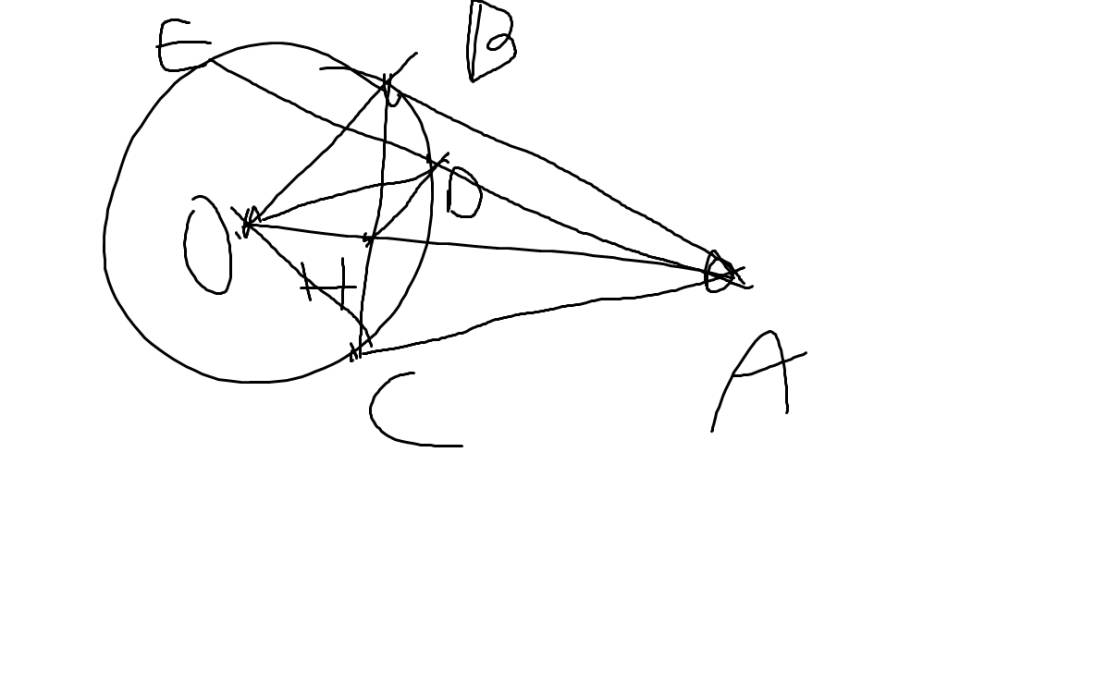
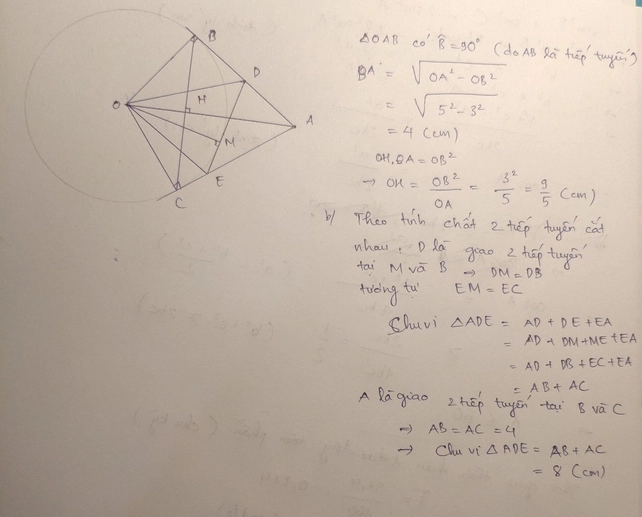 Bài này mk từng làm trên lớp rồi á. Chứ đề bài của bạn phía trên viết thiếu dữ kiện cm.Good luck~
Bài này mk từng làm trên lớp rồi á. Chứ đề bài của bạn phía trên viết thiếu dữ kiện cm.Good luck~