Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án C
Δ P = Δ A Δ t = 480 kWh 24 h = 20 ( kW ) ⇒ H = P - Δ P P = 200 - 20 200 = 90 %
Giải thích: Đáp án B
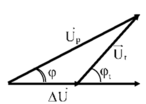
Từ giản đồ vectơ ta có
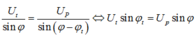
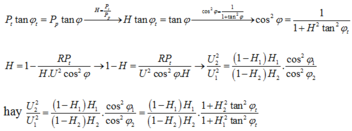
*Áp dụng công thức:
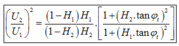
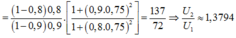
Đáp án B
Phương pháp: Sử dụng công thức hiệu suất truyền tải và tính công suất hao phí
Cách giải: Gọi công suất truyền tải là P, hiệu điện thế phát là U, ta có:
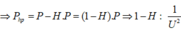
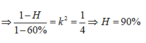
Đáp án: A
- Ban đầu ta có: P 1 = ∆ P + P 2 mà H 1 = 0 , 9 → P 2 = 0 , 9 P 1 = 0 , 9 U I 1 ∆ P 1 = 0 , 1 P 1 → R = 0 , 1 U I 1 (1)
- Sau đó P 1 ' = ∆ P ' + P 2 ' ⇔ U I 2 = R I 2 2 + 1 , 1 P 2 (2)
- Từ (1) và (2) ta có: U I 2 = 0 , 1 U I 2 2 I 1 + 1 , 1 . 0 , 9 U I 1 ⇔ 0 , 1 I 2 I 1 2 - I 2 I 1 + 1 , 1 . 0 , 9 = 0 (3)
- Giải phương trình (3) ta có hai nghiệm: I 2 I 1 = 1 , 114 I 2 I 1 = 8 , 886
- Hiệu suất truyền tải H = P 2 ' P 1 ' = 1 - ∆ P 2 ' P 1 ' = 1 - R I 2 2 U I 2 ⇔ H = 1 - 0 , 1 I 2 I 1 (4)
- Vì hao phí không vượt quá 20% nên ta chọn nghiệm I 2 I 1 = 1,114.
Thay vào (4) ta có H = 88,86%
Đáp án D
+ Phương trình truyền tải điện năng trong hai trường hợp: 
Với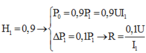 
+ Thay vào phương trình truyền tải thứ hai (lưu ý rằng điện áp nơi truyền đi là như nhau) ta thu được phương trình:
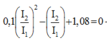Phương trình cho ta hai nghiệm
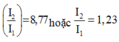
→ Hiệu suất truyền tải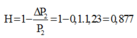 
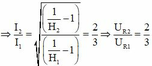
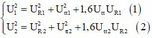
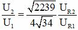
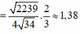
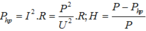
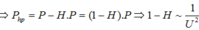
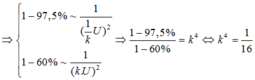
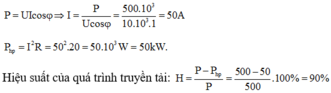
Đáp án C
Sử dụng lí thuyết về truyền tải điện năng
Cách giải: Công suất hao phí ∆ P = ∆ A t = 480 24 = 20 k W
Hiệu suất của quá trình truyền tải H = 1 - ∆ P P = 1 - 20 200 = 0 , 9 ( 90 % )