Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:Ta có:
a) \(\left|x-3\right|=5\Leftrightarrow\left[{}\begin{matrix}x-3=5\\x-3=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
b) \(\left|2x+3\right|=2.\left|4-x\right|\)
+)Xét \(\left\{{}\begin{matrix}2x+3\ge0\\4-x\ge0\end{matrix}\right.\) \(\Leftrightarrow\dfrac{-3}{2}\le x\le4\)
Khi đó \(2x+3=2\left(4-x\right)\Leftrightarrow2x+3=8-2x\Leftrightarrow4x=5\Leftrightarrow x=\dfrac{5}{4}\left(tm\right)\)
+) Xét \(\left\{{}\begin{matrix}2x+3\ge0\\4-x\le0\end{matrix}\right.\) \(\Leftrightarrow x\ge4\)
Khi đó: \(2x+3=2\left(x-4\right)=2x-8\Leftrightarrow0x=-11\left(vl\right)\)
+) Xét \(\left\{{}\begin{matrix}2x+3\le0\\4-x\ge0\end{matrix}\right.\) \(\Leftrightarrow x\le\dfrac{-3}{2}\)
Khi đó: \(-\left(2x+3\right)=2.\left(4-x\right)\Leftrightarrow-2x-3=8-2x\left(vl\right)\)
+)Xét \(\left\{{}\begin{matrix}2x+3\le0\\4-x\le0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{-3}{2}\\x\ge4\end{matrix}\right.\) \(\left(vl\right)\)
Vậy...
c) ĐKXĐ : \(3-x\ge0\Leftrightarrow x\le3\)
+)Xét \(x^{^2}-3x+1\ge0\)
\(\Leftrightarrow x^2-3x+1=3-x\Leftrightarrow x^2-2x-2=0\)
\(\Leftrightarrow x^2-2x+1=3\Leftrightarrow\left(x-1\right)^2=3\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=\sqrt{3}\\x-1=-\sqrt{3}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1+\sqrt{3}\left(tm\right)\\x=1-\sqrt{3}\left(tm\right)\end{matrix}\right.\)
+)Xét \(x^{^2}-3x+1\le0\)
\(\Leftrightarrow-\left(x^2-3x+1\right)=3-x\)
\(\Leftrightarrow x^2-3x+1=x-3\Leftrightarrow x^2-4x+4=0\)
\(\Leftrightarrow\left(x-2\right)^2=0\Leftrightarrow x-2=0\Leftrightarrow x=2\left(tm\right)\)
Vậy...
Câu 2:
Ta có:
Phương trình \(\left(x+3\right)\left(x^2-2x+m-1\right)=0\) có một nghiệm là \(x=-3\)
\(\Rightarrow\)Phương trình \(\left(x+3\right)\left(x^2-2x+m-1\right)=0\) có ba nghiệm phân biệt khi và chỉ khi \(x^2-2x+m-1=0\) có 2 nghiệm phân biệt và khác \(-3\)
Ta có: \(x^2-2x+m-1=0\) có 2 nghiệm phân biệt khi và chỉ khi \(\text{△}>0\Leftrightarrow8-4m>0\Leftrightarrow m< 2\)
Gọi \(x_1\) và \(x_2\) là 2 nghiệm của phương trình \(x^2-2x+m-1=0\).Theo hệ thức Vi-ét ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{-2}{1}=2\\x_1x_2=\dfrac{m-1}{1}=m-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_1=2-x_2\\\left(2-x_2\right).x_2=m-1\end{matrix}\right.\)
Nếu \(x_2\ne-3\) thì \(m-1\ne-15\Leftrightarrow m\ne-14\).
Do vai trò của \(x_1\) và \(x_2\) là như nhau nên \(x^2-2x+m-1=0\) có 2 nghiệm phân biệt và khác \(-3\) khi và chỉ khi: \(\left\{{}\begin{matrix}m< 2\\m\ne-14\end{matrix}\right.\)

a) \(2{x^2} + 3x + 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = 2{x^2} + 3x + 1\) có 2 nghiệm phân biệt \(x = - 1,x = \frac{{ - 1}}{2}\)
hệ số \(a = 2 > 0\)
Ta có bảng xét dấu f(x) như sau:
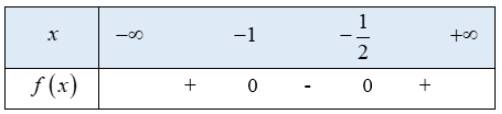
Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \le - 1\\x \ge - \frac{1}{2}\end{array} \right.\)
Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right] \cup \left[ { - \frac{1}{2}; + \infty } \right)\)
b) \( - 3{x^2} + x + 1 > 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + x + 1\) có 2 nghiệm phân biệt \(x = \frac{{1 - \sqrt {13} }}{6},x = \frac{{1 + \sqrt {13} }}{6}\)
Hệ số \(a = - 3 < 0\)
Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy \(f\left( x \right) > 0\)\( \Leftrightarrow \frac{{1 - \sqrt {13} }}{6} < x < \frac{{1 + \sqrt {13} }}{6}\)
Vậy tập nghiệm của bất phương trình là \(\left( {\frac{{1 - \sqrt {13} }}{6};\frac{{1 + \sqrt {13} }}{6}} \right)\)
c) \(4{x^2} + 4x + 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = 4{x^2} + 4x + 1\) có nghiệm duy nhất \(x = \frac{{ - 1}}{2}\)
hệ số \(a = 4 > 0\)
Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow x \in \mathbb{R}\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\)
d) \( - 16{x^2} + 8x - 1 < 0\)
Tam thức bậc hai \(f\left( x \right) = - 16{x^2} + 8x - 1\) có nghiệm duy nhất \(x = \frac{1}{4}\)
hệ số \(a = - 16 < 0\)
Ta có bảng xét dấu f(x) như sau:
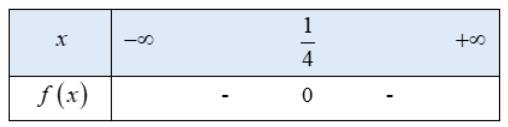
Từ bảng xét dấu ta thấy \(f\left( x \right) < 0 \Leftrightarrow x \ne \frac{1}{4}\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\backslash \left\{ {\frac{1}{4}} \right\}\)
e) \(2{x^2} + x + 3 < 0\)
Ta có \(\Delta = {1^2} - 4.2.3 = - 23 < 0\) và có \(a = 2 > 0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \(2{x^2} + x + 3\) mang dấu “-” là \(\emptyset \)
Vậy tập nghiệm của bất phương trình \(2{x^2} + x + 3 < 0\) là \(\emptyset \)
g) \( - 3{x^2} + 4x - 5 < 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + 4x - 5\) có \(\Delta ' = {2^2} - \left( { - 3} \right).\left( { - 5} \right) = - 11 < 0\) và có \(a = - 3 < 0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \( - 3{x^2} + 4x - 5\) mang dấu “-” là \(\mathbb{R}\)
Vậy tập nghiệm của bất phương trình \( - 3{x^2} + 4x - 5 < 0\) là \(\mathbb{R}\)

a: Để phương trình có hai nghiệm trái dấu thì m+2<0
hay m<-2

a) \(2{x^2} - 3x + 1 > 0\)
Tam thức \(f\left( x \right) = 2{x^2} - 3x + 1\) có \(a + b + c = 2 - 3 + 1 = 0\) nên hai nghiệm phân biệt \({x_1} = 1\) và \({x_2} = \frac{1}{2}.\)
Mặt khác \(a = 2 > 0,\) do đó ta có bảng xét dấu sau:

Tập nghiệm của bất phương trình là: \(S= \left( { - \infty ;\frac{1}{2}} \right) \cup \left( {1; + \infty } \right).\)
b) \({x^2} + 5x + 4 < 0\)
Tam thức \(f\left( x \right) = {x^2} + 5x + 4\) có \(a - b + c = 1 - 5 + 4 = 0\) nên phương trình có hai nghiệm phân biệt \(x = - 1\) và \(x = - 4.\)
Mặt khác \(a = 1 > 0,\) do đó ta có bảng xét dấu sau:

Tập nghiệm của bất phương trình là: \(S = \left( { - 4; - 1} \right).\)
c) \( - 3{x^2} + 12x - 12 \ge 0\)
Tam thức \(f\left( x \right) = - 3{x^2} + 12x - 12 = - 3\left( {{x^2} - 4x + 4} \right) = - 3{\left( {x - 2} \right)^2} \le 0\)
Do đó
\( - 3{x^2} + 12x - 12 \ge 0 \Leftrightarrow - 3{x^2} + 12x - 12 = 0 \Leftrightarrow - 3{\left( {x - 2} \right)^2} = 0 \Leftrightarrow x = 2.\)
Tập nghiệm của bất phương trình là: \(S = \left( { 2} \right).\)
d) \(2{x^2} + 2x + 1 < 0.\)
Tam thức \(f\left( x \right) = 2{x^2} + 2x + 1\) có \(\Delta = - 1 < 0,\) hệ số \(a = 2 > 0\) nên \(f\left( x \right)\) luôn dướng với mọi \(x,\) tức là \(2{x^2} + 2x + 1 > 0\) với mọi \(x \in \mathbb{R}.\)
\( \Rightarrow \) bất phương trình vô nghiệm

Phương án A có nhiều giá trị quá, thay vào phương trình mất nhiều thời gian, nên ta xét các phương trình còn lại.
Với phương án B, khi thay x = 0 vào phương trình thì hai vế đều bằng 4 nên x = 0 là một nghiệm. Tuy nhiên khi thay giá trị x = 4 vào phương trình thì vế trái bằng 0, còn vế phải bằng 16. Vậy phương án B và phương án C đều bị loại. Với phương án D, giá trị x = 1 cũng không phải là nghiệm của phương trình, nên phương án D bị loại.
Đáp án: A
 là:
là: x + y = -1 B.
x + y = -1 B. 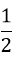 x - y = -1
x - y = -1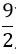 ) D.(2; 2) và (-3;
) D.(2; 2) và (-3;
Điều kiện xác định x + 2 ≥ 0 x ≠ 0 x 2 + 3 x − 4 ≠ 0 ⇔ x ≥ − 2 x ≠ 1 x ≠ 0 x ≠ − 4 ⇔ x ∈ [ - 2 ; + ∞ ) \ 0 ; 1
Đáp án cần chọn là: C