Định lý Pytago: trong một tam giác vuông, tổng bình phương 2 cạnh góc vuông bằng bình phương cạnh huyền.

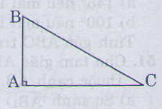
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

∆ABC vuông tại A.

=>  BC2=AB2+AC2

Tham khảo nhé:

Câu hỏi của Uyên Trần - Toán lớp 7 - Học toán với OnlineMath

hình vẽ minh họa

Giả thiết : a//c ; b//c

Kết luận : a//b

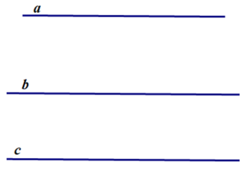
Hình minh họa và viết giả thiết kết luận bằng kí hiệu:

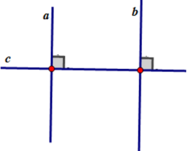
Giả thiết: a⊥c, b⊥c

Kết luận: a//b

a)

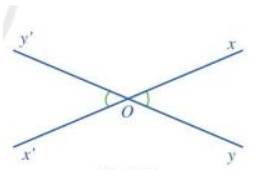
b)

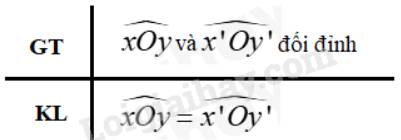
c) Vì góc xOy và x’Oy’ là hai góc đối đỉnh nên Oy và Oy’ là hai tia đối nhau; Ox và Ox’ là hai tia đối nhau

\( \Rightarrow \widehat {xOy}\) và \(\widehat {xOy'}\) là hai góc kề bù; \(\widehat {xOy'}\) và \(\widehat {x'Oy'}\) là hai góc kề bù

\( \Rightarrow \widehat {xOy} + \widehat {xOy'} = 180^\circ \); \(\widehat {xOy'} + \widehat {x'Oy'} = 180^\circ \) ( tính chất 2 góc kề bù)

\( \Rightarrow \)\(\widehat {xOy} = \widehat {x'Oy'}\) (đpcm)

Định lí Pytago thuận.

Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

∆ABC vuông tại A.

=> BC²=AB²+AC²

Định lí Pytago đảo.

Nếu một tam giác có bình phương của một cạnh bẳng tổng bình phương các cạnh còn lại thì tam giác đó là tam giác vuông.

∆ABC :BC²=AB²+AC²

=> góc BAC=90²

thuận

Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

đảo

Nếu một tam giác có bình phương của một cạnh bẳng tổng bình phương các cạnh còn lại thì tam giác đó là tam giác vuông.

a) Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia. còn hình thì mình gửi luôn

câu b đâu bạn ?

có hàng trăm cách rất nhiều

có 2 định lí pi- ta- go là

+ Định lí pi-ta-go thường

trong một tam giác vuông ,bình phuong của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông

+ Định lí pi-ta-go đảo

nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông