Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
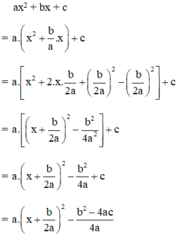
Ta có: a > 0 (gt),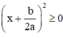 
với mọi x, a, b ⇒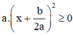 
Phương trình ax2 + bx + c = 0 vô nghiệm nên
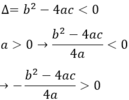
Vậy
a
x
2
+
b
x
+
c
= 
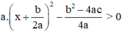với mọi x.
Khi a > 0 và phương trình vô nghiệm thì b2 – 4ac < 0.
Do đó: > 0
Suy ra: ax2 + bx + c = a > 0, với mọi x.
Vì PTVN nên Δ<0
=>f(x)=ax^2+bx+c luôn cùng dấu với a
=>f(x)>0 với mọi x
Xét phương trình bậc hai một ẩn
ax2 + bx + c = 0 (a ≠ 0) và biệt thức = b2 – 4ac
TH1: Nếu < 0 thì phương trình vô nghiệm
TH2. Nếu = 0 thì phương trình có nghiệm
kép x1 = x2 = − b 2 a
TH3: Nếu > 0 thì phương trình có
hai nghiệm phân biệt x1, 2 = − b ± Δ 2 a
Đáp án cần chọn là: A
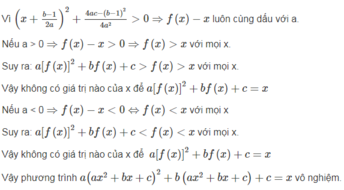
Ta có: a > 0 (gt),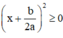
với mọi x, a, b ⇒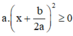 
Phương trình ax2 + bx + c = 0 vô nghiệm nên
Vậy ax2 + bx + c =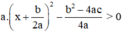
với mọi x.