Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét hàm số \(y=ax^4+bx^2+c\)
Ta có \(y'=4ax^3+2bx=2x\left(2ax^2+b\right)\)
\(y'=0\Leftrightarrow x=0\) hoặc \(2ax^2+b=0\left(1\right)\)
Đồ thị hàm số có 3 cực trị phân biệt khi và chỉ khi \(y'=0\) có 3 nghiệm phân biệt hay phương trình (1) có 2 nghiệm phân biệt khác 0 \(\Leftrightarrow ab< 0\) (*)
Với điều kiện (*) thì đồ thị có 3 điểm cực trị là :
\(A\left(0;c\right);B\left(-\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right);C\left(\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right)\)
Ta có \(AB=AC=\sqrt{\frac{b^2-8ab}{16a^2}};BC=\sqrt{-\frac{2b}{a}}\) nên tam giác ABC vuông khi và chỉ khi vuông tại A.
Khi đó \(BC^2=2AB^2\Leftrightarrow b^3+8a=0\)
Do đó yêu cầu bài toán\(\Leftrightarrow\begin{cases}ab< 0\\b^3+8a=0\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\-8\left(m+1\right)^3+8=0\end{cases}\)\(\Leftrightarrow m=0\)
b) Ta có yêu cầu bài toán \(\Leftrightarrow\begin{cases}ab< 0\\OA=BC\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\m^2-4\left(m+1\right)=0\end{cases}\)
\(\Leftrightarrow m=2\pm2\sqrt{2}\)

Chọn D
Ta có: y ' = 3 x 2 - 4 x , y ' ' = 6 x - 4 ;
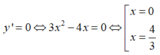
y''(0) = -4 < 0; y''(4/3) = 4 > 0. Do đó hàm số có hai cực trị là x = 0 và x = 4/3
Các mệnh đề (1); (2) và (3) sai;mệnh đề (4) đúng.

Lời giải:
$y'=3x^2-6mx+3(m^2-1)=0$
$\Leftrightarrow x^2-2mx+m^2-1=0$
$\Leftrightarrow x=m+1$ hoặc $x=m-1$
Với $x=m+1$ thì $y=-2m-2$. Ta có điểm cực trị $(m+1, -2m-2)$
Với $x=m-1$ thì $y=2-2m$. Ta có điểm cực trị $m-1, 2-2m$
$f''(m+1)=6>0$ nên $A(m+1, -2m-2)$ là điểm cực tiểu
$f''(m-1)=-6< 0$ nên $B(m-1,2-2m)$ là điểm cực đại
$BO=\sqrt{2}AO$
$\Leftrightarrow BO^2=2AO^2$
$\Leftrightarrow (m-1)^2+(2-2m)^2=2(m+1)^2+2(-2m-2)^2$
$\Leftrightarrow m=-3\pm 2\sqrt{2}$

ta tính \(y'=4x^3-2\left(3m-1\right)x=2x\left(2x^2-3x+1\right)\)
để hàm số có 3 cực trị thì pt y'=0 có 3 nghiệm phân biệt
ta có
\(y'=0\Leftrightarrow2x\left(2x^2-3m+1\right)=0\Rightarrow x=0;2x^2=3m-1\)
để pt có 3 nghiệm phân biệt thì 3m-1>0 suy ra m>1/3
x=0 ta có y=2m+1 suy ra \(A\left(0;2m+1\right)\) ;\(B\left(\sqrt{\frac{3m-1}{2}};-\frac{\left(3m-1\right)^2}{4}+2m+1\right)\); \(C\left(-\sqrt{\frac{3m-1}{2}};\frac{-\left(3m-1\right)^2}{4}+2m+1\right)\)
ta có \(\vec{AB}\left(\sqrt{\frac{3m-1}{2}};\frac{-\left(3m-1\right)^2}{4}\right)\); \(\vec{AC}=\left(-\sqrt{\frac{3m-1}{2}};-\frac{\left(3m-1\right)^2}{4}\right)\)
suy ra AC=AB suy ra tam giác ABC cân tại A
Gỉa sử A,B,C,D nội tiếp đường tròn suy ra tâm của đường tròn nằm trên trung tuyến BC
do tam giác ABC cân tại A suy ra trung tuyến BC cũng chính là đường cao của BC
ta có
\(\vec{BC}=\left(2\sqrt{\frac{3m-1}{2}};0\right)\)
phương trình đường cao qua A và vuông góc với BC nhận \(\vec{BC}\)làm vecto pháp tuyến có dạng
\(2\sqrt{\frac{3m-1}{2}}\left(x-0\right)+0\left(y-2m-1\right)=0\Rightarrow x=0\)(d)
Gọi I(0;a) thuộc (d) là tâm đường tròn mà A,B,C,D nội tiếp
suy ra ta có hệ pt
\(\begin{cases}IA=IB\\IB=IC\\IC=ID\end{cases}\)
giải ra ta tim đc m
Chọn đáp án C.
Ta có y ' = 3 x 2 - 2 ( m + 1 ) x + m 2 - 2
trước tiên ta phải có phương trình y ' = 0 có hai nghiệm phân biệt
![]()
![]()
Điều kiện hai điểm cực trị của đồ thị hàm số nằm cùng về một phía đối với trục hoành là y x 1 . y x 2 > 0
⇔ y = 0 có đúng một nghiệm thực.
Thử trực tiếp các giá trị của m∈{−1,0,1,2} nhận các giá trị m∈{−1,0,2} để y = 0 có đúng một nghiệm thực.

+ Đạo hàm y’ = -3x2+ 6x+ 3( m2-1) = -3( x2- 2x-m2+1).
Đặt g( x) = x2- 2x-m2+1 là tam thức bậc hai có ∆ ' = m 2 .
+ Do đó hàm số đã cho có cực đại cực tiểu khi và chỉ khi y’ =0 có hai nghiệm phân biệt hay g(x) =0 có hai nghiệm phân biệt
⇔ ∆ ' > 0 ⇔ m ≠ 0 . (1)
+ Khi đó y’ có các nghiệm là: 1±m .
Tọa độ các điểm cực trị của đồ thị hàm số là A( 1-m ; -2-2m3) và B( 1+m ; -2+ 2m3).
Ta có:
O A → ( 1 - m ; - 2 - 2 m 3 ) ⇒ O A 2 = ( 1 - m ) 2 + 4 ( 1 + m 3 ) 2 . O B → ( 1 + m ; - 2 + 2 m 3 ) ⇒ O B 2 = ( 1 + m ) 2 + 4 ( 1 - m 3 ) 2 .
Để A và B cách đều gốc tọa độ khi và chỉ khi OA= O B hay OA2= OB2
( 1 - m ) 2 + 4 ( 1 + m 3 ) 2 = ( 1 + m ) 2 + 4 ( 1 - m 3 ) 2 ⇔ - 4 m + 16 m 3 = 0
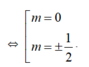
Đối chiếu với điều kiện (1), ta thấy chỉ m = ± 1 2 thỏa mãn yêu cầu bài toán.
Vậy không có giá trị nguyên nào của m thỏa mãn yêu cầu bài toán.
Chọn A.

Đáp án A
Hàm số
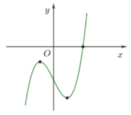
là hàm số chẵn và đồ thị của nó được suy ra từ đồ thị hàm số y = x 3 - 3 x 2 + 1 bằng cách bỏ đi phần bên trái trục tung. Giữ nguyên phần bên phải trục tung và lấy đối xứng với phần bên phải Oy qua Oy.
Như vậy ta sẽ thu được đồ thị hàm số y = x 3 - 3 x 2 + 1 có dạng như sau: