Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Để thỏa mãn tính chất tiếp tuyến của đồ thị hàm số tại điểm có hoành độ là nghiệm của phương trình y ' ' x = 0 là một đường thẳng song song với trục hoành thì hàm số phải thỏa mãn điều kiện:
Nghiệm của phương trình y ' ' x = 0 là nghiệm của phương trình y ' x = 0 .
Với A: y ' = 3 x 2 − 6 x + 1 ; y ' ' = 6 x − 6 .
y ' ' = 0 ⇔ x = 1 không là nghiệm của phương trình . y ' = 0 Vậy A không thỏa mãn.
Với B: y ' = 3 x 2 − 6 x − 1 ; y ' ' = 6 x − 6 . Tương tự B không thỏa mãn.
Với C: y ' = 3 x 2 − 6 x + 3 ; y ' ' = 6 x − 6 .
y ' ' = 0 ⇔ x = 1 là nghiệm của phương trình y ' = 0 thỏa mãn, vậy ta chọn C.

Chọn đáp án B


FOR REVIEW |
Sai lầm thường gặp trong bài toán là vội vàng kết luận số tiếp tuyến thỏa mãn yêu cầu bài toán bằng số tiếp điểm khi chưa viết phương trình tiếp tuyến. |

Đáp án B.
Ta có y ' = 3 x 2 x - 2 - x 3 x - 2 2 = 2 x 2 x - 3 x - 2 2 .
Do tiếp tuyến song song với trục hoành ⇒ y ' = 0 ⇔ [ x = 0 ⇒ y = - 27 x = 3 ⇒ y = 0
Với x = 3,y = 27 ⇒ PTTT là: y = 0 ≡ O x (loại)
Với x = 0, y = -27 ⇒ PTTT là: y = -27.
Vậy có 1 tiếp tuyến thỏa mãn.

Đáp án B.
Ta có y ' = 4 x 3 − 4 x . Gọi M a ; a 4 − 2 a 2 − 1 là tọa độ tiếp điểm. tiếp tuyến song song với trục hoành thì có hệ số góc bằng 0.
Hệ số góc của tiếp tuyến tại M là
k = y ' a = 4 a 3 − 4 a = 0 ⇔ a = 0 ⇒ M 0 ; − 1 a = 1 ⇒ M 1 ; − 2 a = − 1 ⇒ M − 1 ; − 2
Do đó có 2 tiếp tuyến là y = -1 và y = -2

Đáp án C
Phương pháp : Xét từng mệnh đề.
Cách giải:
(I) sai. Ví dụ hàm số 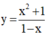 có đồ thị hàm số như sau:
có đồ thị hàm số như sau:
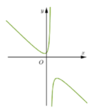 õ ràng
õ ràng ![]()
(II) đúng vì y ' = 4 a x 3 + 2 b x = 0 luôn có một nghiệm x = 0 nên đồ thị hàm số y = a x 4 + b x 2 + c ( a ≠ 0 ) luôn có ít nhất một điểm cực trị
(III) Gọi
x
0
là 1 điểm cực trị của hàm số ![]() => Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ
x
0
là:
=> Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ
x
0
là: ![]() luôn song song với trục hoành.
luôn song song với trục hoành.
Vậy (III) đúng.

Đáp án A.
Hệ số góc tiếp tuyến của đồ thị (C) là
y ' = 0 ⇔ 4 − 4 sin 2 x = 0 ⇔ sin 2 x = 1 ⇔ x = π 4 + k π .
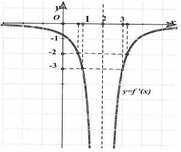



Đáp án B.
Cách 1: Các tiếp tuyến song song với trục hoành có hệ số góc bằng 0
phương trình tiếp tuyến của đồ thị hàm số tại điểm A(0;0) là y = 0, không thỏa mãn.
Vậy có đúng 1 tiếp tuyến song song với trục hoành.
Cách 2:
Tiếp tuyến của đồ thị hàm số song song với trục hoành là các tiếp tuyến tại các điểm cực trị có tung độ khác 0.