Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Hướng dẫn
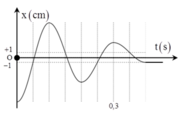
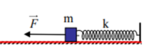
+ Từ hình vẽ, ta có Δ l 0 = F C k = 0 , 01 m → k = 1 0 , 01 = 100 N / m với Δ l 0 là độ biến dạng của lò xo tại vị trí cân bằng tạm.
→ Biên độ dao động của vật trong nửa chu kì thứ nhất A 1 , trong nửa chu kì thứ hai, trong nửa chu kì thứ ba và thứ 4 lần lượt là.
A 1 = A 0 − 1
với A 0 là tọa độ ban đầu của vật
A 2 = A 0 − 3 A 3 = A 0 − 5 A 4 = A 0 − 7 = 2 → A 0 = 9 A 1 = 8 A 2 = 6 A 3 = 4 A 4 = 2
→ Tốc độ cực đại của vật trong quá trình da động v m a x = ω A 1 = 80 π c m / s .
→ Tốc độ trung bình của vật v t b = S t = 2 A 1 + A 2 + A 3 + A 4 t = 2 8 + 6 + 4 + 2 0 , 4 = 100 c m / s
→ Ta có tỉ số v m a x v t b = 0 , 8 π
Đáp án B
Chọn đáp án B.
Do không thay đổi về k, m => ω không đổi.
→ ω = k m = 20 0 , 2 = 10 π ( r a d / s ) .
Ta có năng lượng truyền cho vật là:
E t r u y e n = 1 2 m v 2 = 1 2 .0 , 2.1 2 = 0 , 1 ( J )
⇒ 1 2 k A 2 = E t r u y e n = 0 , 1 ⇒ A = 0 , 1 ( m )
Khi tới biên A lần đầu, năng lượng còn lại là:
=> Biên độ còn lại:
Chọn A
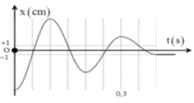
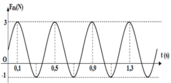
Từ đồ thị ta thấy T = 0,4 s → ω = 5π rad/s.
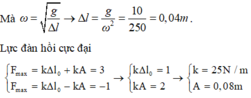
Từ t = 0 đến t = 0,1 s (trong khoảng thời gian T/4) lực đàn hồi tăng đến giá trị cực đại → φ 0 = π 2 rad.
→ Phương trình li độ x = 8cos(5πt + π/2) cm.
Đáp án D
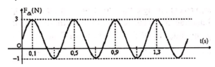
Từ đồ thị ta thấy T = 0,4 s → ω = 5π rad/s.
Mà
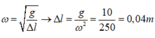
Lực đàn hồi cực đại
Từ t = 0 đến t = 0,1 s (trong khoảng thời gian T/4) lực đàn hồi tăng đến giá trị cực đại
→ 
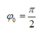rad.
→ Phương trình li độ x = 8cos(5πt + π/2) cm
Đáp án D
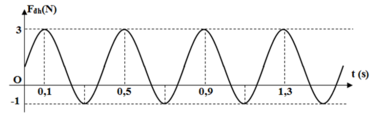
Độ giãn của con lắc ở vị trí cân bằng: T = 0,4 s = 2 π ∆ l 0 g ⇒ ∆ l 0 = T 2 g 4 π 2 = 0 , 04 m = 4 cm
Lực đàn hồi của con lắc tại hai vị trí biên:
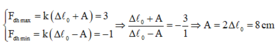
Độ cứng của lò xo: k = F d h m a x ∆ l 0 + A = 3 0 , 04 + 0 , 08 = 25 N / m
Biểu thức lực đàn hồi:
Tại thời điểm t = 0,1 s , lực đàn hồi có giá trị F = 3N nên:
F d h = 1 + 2 cos ( 5 π . 0 , 1 + μ ) = 3
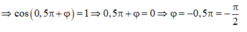
Phương trình dao động của vật: x = 8 cos ( 5 πt - π 2 ) ( c m )
Do vật không chịu tác dụng của lực ma sát, nên cơ năng không đổi,
Khi chịu tác dụng lực thì vật dao động quanh vị trí cân bằng O’ mới. khi ngứng tác dụng lực thì vị trí và vận tốc tại thời điểm đó thay đổi, vị trí cân bằng trở lại vị trí cũ, nhưng cơ năng bảo toàn nên vận tốc cực đại vẫn như cũ
Đáp án C
Đáp án B
Fdhmax = k(∆l + A) → Fdhmax = mω2(∆l + ∆l)
↔ Fdhmax =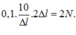 
Giải thích: Đáp án B
Phương pháp : Áp dụng công thức của dao động tắt dần của con lắc lò xo
Cách giải :
+ Từ hình vẽ, ta có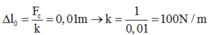
, với ∆l0 là độ biến dạng của lò xo tại vị trí cân bằng tạm.
Biên độ dao động của vật trong nửa chu kỳ thứ nhất A1, trong nửa chu kì thứ hai, trong nửa chu kì thứ ba và thứ 4 lần lượt là:
A1 = A0 – 1, với A0 là tọa độ ban đầu của vật.
→Tốc độ cực đại của vật trong quá trình dao động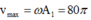
cm/s.
→Tốc độ trung bình của vật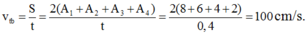
→Ta có tỉ số