Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Số cách chọn 6 học sinh từ 15 học sinh là C 15 6 = 5005(cách)
⇒ n ( Ω ) = 5005
Gọi biến cố A: “Chọn được 6 học sinh đủ 3 khối”
=> A ¯ : “Chọn được 6 học sinh không đủ 3 khối”.
Cách 1
+ Trường hợp 1: Chọn 6 học sinh từ 1 khối 1 => Chọn 6 học sinh khối 10 có C 6 6 = 1 (cách).
+ Trường hợp 2: 6 học sinh được chọn trong 2 khối.
* Chọn 6 học sinh trong khối 11 và khối 12 có ![]() (cách).
(cách).
* Chọn 6 học sinh trong khối 10 và khối 12 có ![]() (cách)
(cách)
* Chọn 6 học sinh trong khối 11 và khối 10 có ![]() (cách).
(cách).
Từ 2 trường hợp suy ra ![]()
.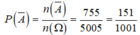
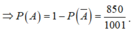 0
0
Cách 2
+ Trường hợp 1: Chọn 6 học sinh từ 1 khối => Chọn 6 học sinh khối 10 có C 6 6 = 1 (cách).
+ Trường hợp 2: 6 học sinh được chọn trong 2 khối có ![]()
Từ 2 trường hợp suy ra ![]()
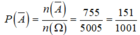
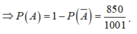

Đáp án A.
Chọn 4 học sinh có C 12 4 cách chọn.
Chọn 4 học sinh trong đó 4 học sinh được chọn có cả 3 khối có:
![]()
Xác xuất để 4 học sinh được chọn có cả 3 khối là P = 270 C 12 4 = 6 11
Do đó xác suất sao cho 4 học sinh được chọn thuộc không quá 2 khối là 1 - 6 11 = 5 11

Đáp án A
Số cách chọn ngẫu nhiên 4 học sinh là C 12 4 = 495
Gọi p là biến cố: 4 học sinh được chọn thuộc không quá 2 khối thì
p ¯ : 4 học sinh được chọn thuộc 3 khối
⇒ p ¯ = 270
⇒ p = 1 - 270 495 = 5 11

Đáp án A
Lấy 8 học sinh trong 19 học sinh có C 19 8 = 75582 cách.
Suy ra số phân tử của không gian mẫu là n ( Ω ) = 75582
Gọi X là biến cố “8 học sinh được chọn có đủ 3 khối”
Xét biến cố đối của biến cố X gồm các trường hợp sau:
+ 8 học sinh được chọn từ 2 khối, khi đó có C 14 8 + C 11 8 + C 13 8 cách.
+ 8 học sinh được chọn từ 1 khối, khi đó có C 8 8 cách.
Do đó, số kết quả thuận lợi cho biển cổ X là n ( X ) = C 19 8 - ( C 14 8 + C 11 8 + C 13 8 + C 8 8 ) = 71128 .
Vậy xác suất cần tính là P = n ( X ) n ( Ω ) = 71128 75582 .

Không gian mẫu là số cách chọn ngẫu nhiên 3 học sinh từ 13 học sinh.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố 3 học sinh được chọn có cả nam và nữ đồng thời có cả khối 11 và khối 12
Ta có các trường hợp thuận lợi cho biến cố A là:
● Trường hợp 1. Chọn 1 học sinh khối 11; 1 học sinh nam khối 12 và 1 học sinh nữ khối 12 nên có ![]() cách.
cách.
● Trường hợp 2. Chọn 1 học sinh khối 11; 2 học sinh nữ khối 12 có ![]() cách.
cách.
● Trường hợp 3. Chọn 2 học sinh khối 11; 1 học sinh nữ khối 12 có ![]() cách.
cách.
Suy ra số phần tử của biến cố A là ![]()
Vậy xác suất cần tính 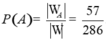
Chọn D.

+ Số cách chọn 6 học sinh bất kỳ từ 18 học sinh là. C 18 6 = 18564
+ Tiếp theo ta đếm số cách chọn ra 6 học sinh từ các học sinh trên mà không có đủ cả ba khối. Khi đó có ba phương án như dưới đây.
Phương án 1: 6 học sinh được chọn thuộc vào khối 10 hoặc 11, số cách chọn là C 13 6 = 1716
Phương án 2: 6 học sinh được chọn thuộc vào cả hai khối 10 và 12, số cách chọn là C 12 6 - C 7 6 = 917
Phương án 3: 6 học sinh được chọn thuộc vào cả hai khối 11 và 12, số cách chọn là C 11 6 - C 6 6 = 461
Vậy số cách chọn 6 học sinh sao cho mỗi khối có ít nhất một học sinh là:
18564 – (1716 + 917 + 461) = 15470.
chọn D.

Đáp án D
Phương pháp:
+ ) P ( A ) = n ( A ) n ( Ω )
+ P(A) = 1P( A )
Cách giải: Số phần tử của không gian mẫu: n ( Ω ) = C 18 6
Gọi A: “Mỗi khối có ít nhất 1 học sinh được chọn.”


Đáp án B.
Số cách chọn 5 em học sinh từ 8 học sinh trên là ![]() cách
cách
- Để chọn 5 em thỏa mãn bài ra, ta xét các trường hợp sau
+) 1 nam khối 11, 1 nữ khối 12 và 3 nam khối 12 có ![]() cách
cách
+) 1 nam khối 11, 2 nữ khối 12 và 2 nam khối 12 có ![]() cách
cách
+) 2 nam khối 11, 1 nữ khối 12 và 2 nam khối 12 có ![]() cách
cách
+) 2 nam khối 11, 2 nữ khối 12 và 1 nam khối 12 có ![]() cách
cách
- Số cách chọn 5 em thỏa mãn bài ra là:
![]() cách
cách
Vậy xác suất cần tính là: ![]()
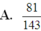
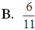

Đáp án D
Chọn 4 học sinh bất kỳ có: Ω = C 13 4 = 715
Gọi A là biến cố: “4 học sinh được chọn có đủ 3 khối”
Khi đó