Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(\left\{{}\begin{matrix}n_{CO_2}=a\left(mol\right)\\n_{H_2O}=b\left(mol\right)\end{matrix}\right.\)
Ta thấy các chất đều có công thức CnH2n+2O \(\Rightarrow n_{O\left(hỗnhợp\right)}=n_{H_2O}-n_{CO_2}\)
\(\Rightarrow n_{O\left(ancol\right)}=b-a\)
Ta có: \(m_{hh}=m_C+m_H+m_O=9,2\left(g\right)\) \(\Rightarrow a+2b+16\left(b-a\right)=9,2\) (1)
Mặt khác: \(n_{O_2}=\dfrac{13,44}{22,4}=0,6\left(mol\right)\)
Bảo toàn oxi: \(\left(b-a\right)+2\cdot0,6=2a+b\) (2)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}a=n_{CO_2}=0,4\left(mol\right)\\b=n_{H_2O}=\dfrac{38}{45}\left(mol\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}V_{CO_2}=0,4\cdot22,4=8,96\left(l\right)\\m_{H_2O}=15,2\left(g\right)\end{matrix}\right.\)

Đáp án A
Ancol no, đơn chức = kCH2 + H2O
Do đó quy đổi X thành:
C3H8O3: a mol
CH2: b mol
H2O: 3a mol
nH2 = 1,5a + 0,5 . 3a = 0,15 => a = 0,05
nH2O = 4a + b + 3a = 0,63 => b = 0,28
=> mX = 92a + 14b + 18.3a = 11,22

Đáp án B
Vì nCH3OH = nC3H7OH => 2 chất này có phân tử khối trung bình bằng ( 32 + 60)/2 = 46 (g/mol)
=> Quy tất cả các chất X về cùng 1 chất có MX = 46 (g/mol)
nH2 = 0,1 (mol) => nX = nH linh động = 2nH2 = 0,2 (mol)
=> mX = 0,2.46 = 9,2 (g)

Đáp án B
Vì nCH3OH = nC3H7OH => 2 chất này có phân tử khối trung bình bằng ( 32 + 60)/2 = 46 (g/mol)
=> Quy tất cả các chất X về cùng 1 chất có MX = 46 (g/mol)
nH2 = 0,1 (mol) => nX = nH linh động = 2nH2 = 0,2 (mol)
=> mX = 0,2.46 = 9,2 (g)

Đáp án B
Vì nCH3OH = nC3H7OH => 2 chất này có phân tử khối trung bình bằng ( 32 + 60)/2 = 46 (g/mol)
=> Quy tất cả các chất X về cùng 1 chất có MX = 46 (g/mol)
nH2 = 0,1 (mol) => nX = nH linh động = 2nH2 = 0,2 (mol)
=> mX = 0,2.46 = 9,2 (g)
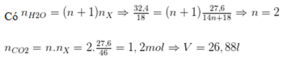
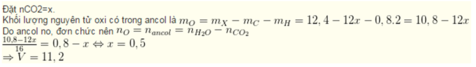
Vì nCH3OH = nC3H7OH
Quy đổi:
\(C_3H_7OH+CH_3OH=2C_2H_5OH\)
Hỗn hợp X chỉ còn là C2H5OH \(C_2H_5OH+3O_2\underrightarrow{^{to}}2CO_2+3H_2O\) \(n_{H2O}=\frac{32,4}{18}=1,8\left(mol\right)\) \(\Rightarrow n_{CO2}=\frac{2}{3}n_{H2O}=1,2\left(mol\right)\) \(\Rightarrow V=V_{CO2}=1,2.22,4=26,88\left(l\right)\)