Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

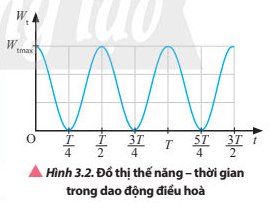
Thế năng của vật đạt giá trị lớn khi ở vị trí hai biên và đạt giá trị nhỏ nhất ở vị trí cân bằng khi vật di chuyển từ vị trí biên đến vị trí cân bằng thế năng của vật giảm dần từ giá trị lớn nhất về 0 và ngược lại.

Công thức (3.5): \(W_d=\dfrac{1}{2}mw^2A^2sin^2\left(wt+\varphi_0\right)\)
Đồ thị động năng – thời gian cũng có dạng hình sin.
Từ đồ thị ta thấy:
+ Tại thời điểm ban đầu, động năng bằng 0
+ Tại thời điểm \(\dfrac{T}{4}\), động năng cực đại
+ Tại thời điểm \(\dfrac{T}{2}\), động năng bằng 0
+ Tại thời điểm \(\dfrac{3T}{4}\), động năng cực đại
+ Tại thời điểm T, động năng bằng 0.

Vì điện trở của ampe kế ko đáng kể
Nên M trùng N
MCD:R1nt(R2//R4)nt(R3//R5)
a,\(R_{24}=\dfrac{R_2\cdot R_4}{R_2+R_4}=\dfrac{4\cdot5}{4+5}=\dfrac{20}{9}\left(\Omega\right)\)
\(R_{35}=\dfrac{R_3\cdot R_5}{R_3+R_5}=\dfrac{6\cdot10}{6+10}=3,75\left(\Omega\right)\)
\(R_{tđ}=R_1+R_{24}+R_{35}=2+\dfrac{20}{9}+3,75=\dfrac{287}{36}\left(\Omega\right)\)
\(I_1=I_{24}=I_{35}=I=\dfrac{U}{R_{tđ}}=\dfrac{40}{\dfrac{287}{36}}=\dfrac{1440}{287}\left(A\right)\)
\(U_2=U_4=U_{24}=I_{24}\cdot R_{24}=\dfrac{1440}{287}\cdot\dfrac{20}{9}=\dfrac{3200}{287}\left(V\right)\)
\(U_3=U_5=U_{35}=I_{35}\cdot R_{35}=\dfrac{1440}{287}\cdot3,75=\dfrac{5400}{287}\left(V\right)\)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{\dfrac{3200}{287}}{4}=\dfrac{800}{287}\left(A\right)\)
\(I_3=\dfrac{U_3}{R_3}=\dfrac{\dfrac{5400}{287}}{6}=\dfrac{900}{287}\left(A\right)\)
\(I_4=\dfrac{U_4}{R_4}=\dfrac{\dfrac{3200}{287}}{5}=\dfrac{640}{287}\left(A\right)\)
\(I_5=\dfrac{U_5}{R_5}=\dfrac{\dfrac{5400}{287}}{10}=\dfrac{540}{287}\left(A\right)\)
\(U_1+U_2+U_{MN}+U_5=U\Leftrightarrow R_1I_1+U_2+U_{MN}+U_5=U\)
\(\Rightarrow2\cdot\dfrac{1440}{287}+\dfrac{3200}{287}+U_{MN}+\dfrac{3200}{287}=40\Leftrightarrow U_{MN}=\dfrac{2200}{287}\left(V\right)\)

F là lực giữa hai điện tích (N)
k là hằng số Coulomb \(k=9\cdot10^9Nm^2/C^2\)
\(q_1,q_2\) là điện tích (C)
\(r\) khoảng cách giữa hai điện tích (m)
\(\varepsilon_0\) là hằng số điện \(\varepsilon_0=8,85\cdot10^{-12}C^2/Nm^2\)


Ta có:
\(W_t=\dfrac{1}{2}m\omega^2A^2cos^2\left(\omega t+\varphi_0\right)\\ W_d=\dfrac{1}{2}mv^2=\dfrac{1}{2}m\omega^2A^2sin^2\left(\omega t+\varphi_0\right)\\ \Rightarrow W=W_t+W_d=\dfrac{1}{2}m\omega^2A^2\left[cos^2\left(\omega t+\varphi_0\right)+sin^2\left(\omega t+\varphi_0\right)\right]\\ \Rightarrow W=\dfrac{1}{2}m\omega^2A^2\)