Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Dựa trên mã lệnh thuật toán cho trong Hình 3.

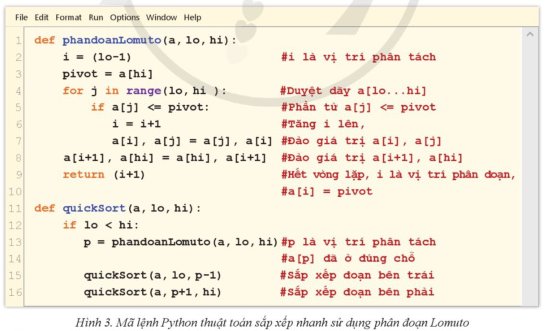
b) Dựa trên mã lệnh thuật toán cho trong Hình 5.


# Nhập dãy số từ bàn phím
lst = list(map(int, input("Nhập dãy số cách nhau bởi dấu cách: ").split()))
# Sắp xếp dãy số theo thuật toán sắp xếp chọn
for i in range(len(lst)):
min_idx = i
for j in range(i+1, len(lst)):
if lst[j] < lst[min_idx]:
min_idx = j
lst[i], lst[min_idx] = lst[min_idx], lst[i]
# In kết quả ra màn hình
print("Dãy số đã sắp xếp:", lst)

#include <bits/stdc++.h>
using namespace std;
double a[100];
int i,n;
int main()
{
cin>>n;
for (i=1; i<=n; i++) cin>>a[i];
for (i=1; i<=n; i++) cout<<a[i]<<" ";
cout<<endl;
for (i=1; i<=n; i++)
swap(a[i],a[n+1-i]);
for (i=1; i<=n; i++) cout<<a[i]<<" ";
return 0;
}
bn ơi bn làm bằng pascal đc ko ạ, mik cần cả hai cái lun

Tham khảo:
a) Gợi ý:
Ý tưởng
Dùng một vòng do while để nhập a, b, c nếu a = 0, thì nhập lại.
Chúng ta dùng hàm sqrt() trong thư viện math.h để tính căn delta hoặc tính căn không dùng hàm sqrt()tại đây.
Chúng ta tạo hàm giaiPT trả về kiểu int chính là số nghiệm của phương trình (1).
Chúng ta sẽ đưa tham chiếu 2 biến x1 , x2 vào hàm giaiPT để gán giá trị hai nghiệm.
Nếu pt (1) vô nghiện thì giaiPT sẽ trả về 0 , đồng thời gán x1 = x2 =0 .
Nếu pt (1) có nghiệm kép thì giaiPT sẽ trả về 1 , đồng thời gán x1 = x2 = -b/2a .
Nếu pt (1) có 2 nghiệm thì giaiPT sẽ trả về 2 , gán x1 = (-b+√delta ) / 2a x = (-b-√delta ) / 2a .
b) Gợi ý:
#include <iostream>
using namespace std;
void nhap(int &n, int a[]){
for(int i=0;i<n;i++){
cout<<"a["<<i+1<<"]= ";cin>>a[i];
}
}
void xuat(int n, int a[]){
for(int i=0;i<n;i++){
cout<<a[i]<<" ";
}
}
int tinhTBCongint (int n, int a[]){
int sum=0, dem=0;
for(int i=0;i<n;i++){
sum+=a[i]; dem++;
}
return sum/n;
}
int tinhTBCongDuong(int n, int a[]){
int sum=0, dem=0;
for(int i=0;i<n;i++){
if(a[i] > 0) {
sum+=a[i]; dem++;
}
}
if(dem==0) return 0;
return sum/dem;
}
int tinhTBCongAm(int n, int a[]){
int sum=0, dem=0;
for(int i=0;i<n;i++){
if(a[i]<0) {
sum+=a[i]; dem++;
}
}
if(dem==0) return 0;
return sum/dem;
}
int main(){
int n;
int a[100];
do{
cout<<"Nhap n: "; cin>>n;
}while(n <= 0 || n >=100);
nhap(n,a);
cout<<"\n--------XUAT MANG----\n";
xuat(n,a);
cout<<"Trung binh cong: "<<tinhTBCongint(n,a)<<"\n\n";
cout<<"Trung binh so duong: "<<tinhTBCongDuong(n,a)<<"\n\n";
cout<<"Trung binh so am: "<<tinhTBCongAm(n,a)<<"\n\n";
}

Tham khảo:
a) Gợi ý:
Ý tưởng
Dùng một vòng do while để nhập a, b, c nếu a = 0, thì nhập lại.
Chúng ta dùng hàm sqrt() trong thư viện math.h để tính căn delta hoặc tính căn không dùng hàm sqrt()tại đây.
Chúng ta tạo hàm giaiPT trả về kiểu int chính là số nghiệm của phương trình (1).
Chúng ta sẽ đưa tham chiếu 2 biến x1 , x2 vào hàm giaiPT để gán giá trị hai nghiệm.
Nếu pt (1) vô nghiện thì giaiPT sẽ trả về 0 , đồng thời gán x1 = x2 =0 .
Nếu pt (1) có nghiệm kép thì giaiPT sẽ trả về 1 , đồng thời gán x1 = x2 = -b/2a .
Nếu pt (1) có 2 nghiệm thì giaiPT sẽ trả về 2 , gán x1 = (-b+√delta ) / 2a x = (-b-√delta ) / 2a .
b) Gợi ý:
#include <iostream>
using namespace std;
void nhap(int &n, int a[]){
for(int i=0;i<n;i++){
cout<<"a["<<i+1<<"]= ";cin>>a[i];
}
}
void xuat(int n, int a[]){
for(int i=0;i<n;i++){
cout<<a[i]<<" ";
}
}
int tinhTBCongint (int n, int a[]){
int sum=0, dem=0;
for(int i=0;i<n;i++){
sum+=a[i]; dem++;
}
return sum/n;
}
int tinhTBCongDuong(int n, int a[]){
int sum=0, dem=0;
for(int i=0;i<n;i++){
if(a[i] > 0) {
sum+=a[i]; dem++;
}
}
if(dem==0) return 0;
return sum/dem;
}
int tinhTBCongAm(int n, int a[]){
int sum=0, dem=0;
for(int i=0;i<n;i++){
if(a[i]<0) {
sum+=a[i]; dem++;
}
}
if(dem==0) return 0;
return sum/dem;
}
int main(){
int n;
int a[100];
do{
cout<<"Nhap n: "; cin>>n;
}while(n <= 0 || n >=100);
nhap(n,a);
cout<<"\n--------XUAT MANG----\n";
xuat(n,a);
cout<<"Trung binh cong: "<<tinhTBCongint(n,a)<<"\n\n";
cout<<"Trung binh so duong: "<<tinhTBCongDuong(n,a)<<"\n\n";
cout<<"Trung binh so am: "<<tinhTBCongAm(n,a)<<"\n\n";
}

a. Ví dụ một bài toán tìm kiếm trong thực tế: Giáo viên muốn tìm tên bạn Chung trong danh sách lớp sau:

Các bước thực hiện thuật toán tìm kiếm nhị phân cho bài toán trên:
- Bước 1: Xét vị trí ở giữa dãy, đó là vị trí số 5
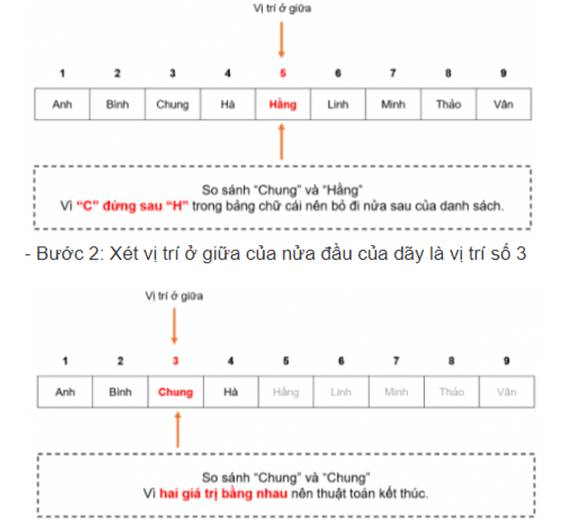
- Vì sau bước 2 đã tìm thấy tên học sinh nên thuật toán kết thúc.
b) Thuật toán tìm kiếm nhị phân
- Thuật toán tìm kiếm nhị phân thu hẹp được phạm vi tìm kiếm chỉ còn tối đa là một nửa sau mỗi lần lặp. Thuật toán chia bài toán thành những bài toán nhỏ hơn giúp tăng hiệu quả tìm kiếm.
Thuật toán tuần tự
- Mô tả thuật toán phải cụ thể, rõ ràng, đầy đủ, đầu vào là gì, đầu ra là gì và chỉ rõ sự kết thúc thuật toán.
- Cần mô tả thuật toán cho tốt thì người máy hay máy tính mới hiểu đúng và thực hiện được.
- Nếu không, kết quả thực hiện thuật toán có thể không như mong đợi.

uses crt;
var a:array[1..200]of integer;
i,n,j,tam:integer;
begin
clrscr;
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
for i:=1 to n-1 do
for j:=i+1 to n do
if a[i]<a[j] then
begin
tam:=a[i];
a[i]:=a[j];
a[j]:=tam;
end;
for i:=1 to n do
write(a[i]:4);
readln;
end.

Diễn biến từng bước sắp xếp nhanh một dãy số cụ thể dùng phân đoạn Lomuto sẽ khác với dùng phân đoạn Hoare. Sự khác biệt giữa phương pháp phân đoạn Lomuto và phân đoạn Hoare trong thuật toán QuickSort là ở việc chọn pivot, cách phân đoạn và cách sắp xếp các phần tử.
Cụ thể, phương pháp phân đoạn Lomuto sẽ chọn pivot là phần tử cuối cùng của mảng, phân đoạn theo pivot và sau đó đưa pivot về giữa hai phân đoạn, tiếp tục thực hiện thuật toán QuickSort trên hai phân đoạn trái và phải của pivot. Trong khi đó, phương pháp phân đoạn Hoare sẽ chọn pivot là phần tử ở giữa mảng, đưa hai con trỏ từ đầu và cuối mảng trỏ tới nhau và dịch chuyển chúng sao cho phần tử bên trái pivot lớn hơn pivot, phần tử bên phải pivot nhỏ hơn pivot, sau đó đưa pivot về vị trí mới và thực hiện QuickSort trên hai phân đoạn trái và phải của pivot.

Tham khảo:
a) Gợi ý
Bước 1: Ta khai báo một mảng tĩnh số nguyên có 100 ô nhớ int a[100].
Bước 2: Ta khai báo số nguyên int n là số lượng phần tử có trong mảng với điều kiện n>1 hoặc n<100 nếu không thỏa mãn thì yêu cầu nhập lại n.
Bước 3: Ta khỏi tạo hàm void Nhap(int a[], int n) dùng để nhập dữ liệu từ bàn phím cho mảng. Trong hàm ta sử dụng vòng for bắt đầu từ int i =0 và kết thúc khi i
Bước 4: Ta khởi tạo hàm void Xuat(int a[], int n) dùng để hiển thị dữ liệu từ mảng ra màn hình. Trong hàm ta sử dụng vòng for bắt đầu từ int i =0 và kết thúc khi i
Bước 5: Ta khởi tạo hàm int TimKiem(int a[], int n) dùng để tìm kiếm phần tử; ta khai báo biến int x là số cần tìm và nhập vào giá trị của x; tiếp theo sử dụng vòng lặp for bắt đầu từ int i =0 và kết thúc khi i
Bước 6: Trong hàm main ta gọi hàm Nhap(a,n), Xuat(a,n) để hiển thị mảng gốc ta gọi thêm hàm TimKiem(a,n) rồi chạy chương trình.
b) Sắp xếp một dãy số giảm dần
#include
int main(){
int a[100];
int n;
printf("\nNhap so luong phan tu n = ");
do{
scanf("%d", &n);
if(n <= 0){
printf("\nNhap lai n = ");
}
}while(n <= 0);
for(int i = 0; i < n; i++){
printf("\nNhap a[%d] = ",i);
scanf("%d", &a[i]);
}
// Sap xep dung thuat toan sap xep chon
int tg;
for(int i = 0; i < n - 1; i++){
for(int j = i + 1; j < n; j++){
if(a[i] < a[j]){
// Hoan vi 2 so a[i] va a[j]
tg = a[i];
a[i] = a[j];
a[j] = tg;
}
}
}
printf("\nMang da sap xep la: ");
for(int i = 0; i < n; i++){
printf("%5d", a[i]);
}
}