Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì mỗi phần tử ở 1 tập hợp đều chỉ xuất hiện 1 lần mà ở tập hợp A lại xuất hiện 4 lần lên 4
=> Tập hợp A = { 1 }
Tập hợp A là tập hợp của con của tập hợp B
Vì phần tử ở tập hợp A đều thuộc tập hợp B
=> A là tập hợp con của B
... Cho em thắc mắc ạ, em không tìm đọc ở đâu có ghi rằng mỗi phần tử ở 1 tập hợp đều chỉ được phép xuất hiện 1 lần.
Nếu theo ý thầy thì đó là dạng tập hợp tổng quát.
Vậy ta phải kết luận là tập hợp tổng quát của A là A1 = { 1 } là tập con của B mới đúng chứ ạ.
Còn A có đến tận 4 số 1, trong khi B chỉ có 1 số 1, nếu thế bản chất là số lượng phần tử số 1 của A lớn hơn số lượng phần tử số 1 của B vậy A không thể là tập con của B ạ.
Khi vẽ ra sơ đồ ta sẽ thấy ngay ạ...
Mong thầy giải đáp giúp ạ



1: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>AC⊥CB
hay OE//AC
Xét ΔOBE vuông tại B có BH là đường cao
nên \(OH\cdot OE=OB^2=R^2\)
2: Xét ΔOBE và ΔOCE có
OB=OC
\(\widehat{BOE}=\widehat{COE}\)
OE chung
Do đó: ΔOBE=ΔOCE
Suy ra: \(\widehat{OBE}=\widehat{OCE}=90^0\)
hay EC là tiếp tuyến của (O)

a)\(\dfrac{2}{3}\sqrt{81}-\dfrac{1}{2}\sqrt{16}=\dfrac{2}{3}.9-\dfrac{1}{2}.4=6+2=8\)
b)\(0,5\sqrt{0,04}+5\sqrt{0,36}=0,5.0,2+5.0,6=0,1+3=3,1\)
c)\(\sqrt{\left(\sqrt{5}-3\right)^2}+\sqrt{\left(\sqrt{5}-13\right)^2}=\sqrt{5}-3+\sqrt{5}-13=2\sqrt{5}-16\)
Câu a em nhầm dấu - thành + ở cuối. Kết quả đúng là 6-2=4

a) Xét (O) có
\(\widehat{BAD}\) là góc nội tiếp chắn \(\stackrel\frown{BD}\)
\(\widehat{CAD}\) là góc nội tiếp chắn \(\stackrel\frown{CD}\)
mà \(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác của \(\widehat{BAC}\))
nên \(\stackrel\frown{BD}=\stackrel\frown{CD}\)
hay BD=CD
Ta có: OB=OC(=R)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: BD=CD(cmt)
nên D nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra OD là đường trung trực của BC
hay OD\(\perp\)BC(đpcm)

a: \(AH=\dfrac{3\sqrt{6}}{5}\left(cm\right)\)
\(AB=\sqrt{AH^2+HB^2}=\dfrac{3\sqrt{10}}{5}\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}=\sqrt{3^2-\left(\dfrac{3\sqrt{10}}{5}\right)^2}=\dfrac{3\sqrt{15}}{5}\left(cm\right)\)

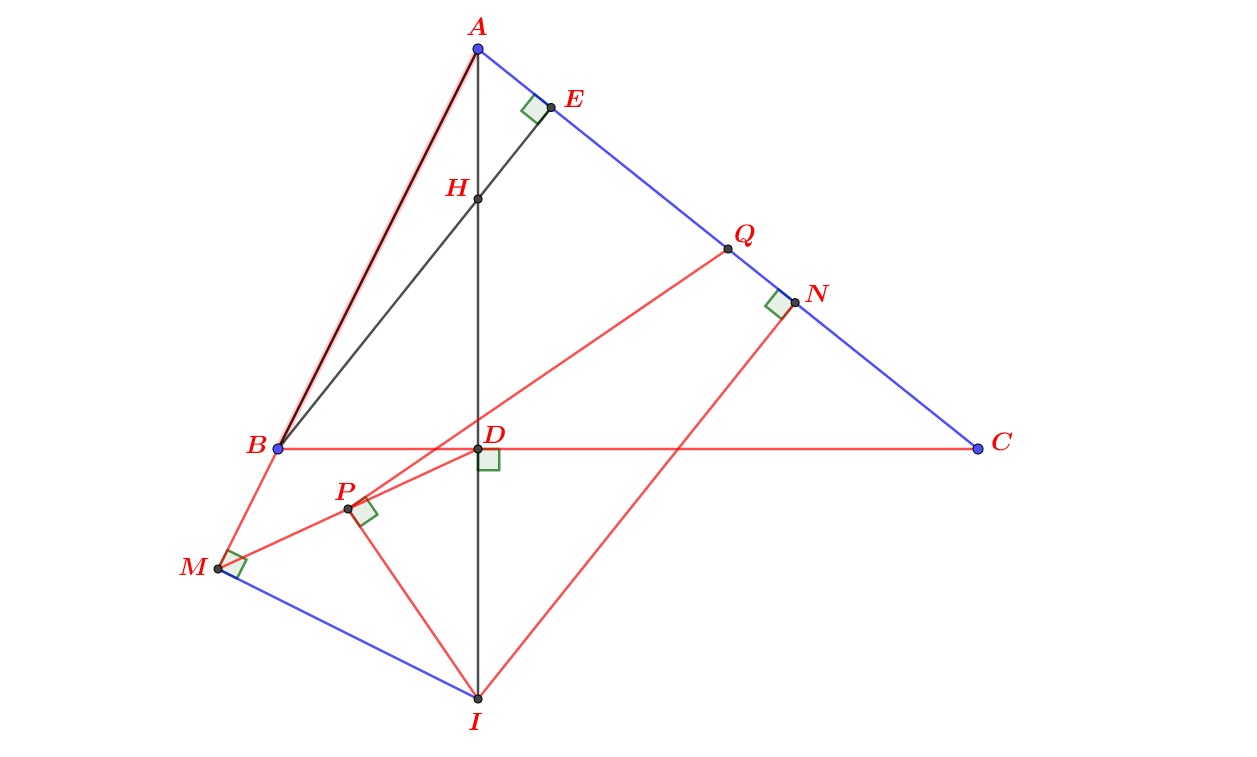









a) Do \(\widehat{EKA}=\widehat{EQA}=90^0\) nên \(AQKE\) nội tiếp. Suy ra \(\widehat{KQE}=\widehat{KAE}=\widehat{BCE}.\)
b) Tứ giác \(EDBK\) nội tiếp vì \(\widehat{EDB}=\widehat{EKB}=90^0\). Suy ra:
\(\widehat{EDK}=\widehat{EBK}=\widehat{ECA}\). Vậy thì \(DECN\) nội tiếp
Từ đó \(\widehat{END}=\widehat{ECB}=\widehat{EQK}\) và \(\widehat{DEN}=\widehat{ACB}=\widehat{QAK}=\widehat{KEQ}\)
Suy ra \(\Delta EDN~\Delta EKQ\). Vậy \(\frac{EN}{EQ}=\frac{ND}{QK}\Leftrightarrow EN.QK=ND.EQ\)
c) Ta có \(EF||AO\) vì cùng vuông góc với \(xy\). Do đó:
\(\widehat{EFB}=\widehat{BAO}=\widehat{EAC}=\widehat{EBI}\). Suy ra \(\Delta EIB~\Delta EBF\)
Suy ra \(\frac{EI}{EB}=\frac{EB}{EF}\Leftrightarrow\frac{EI}{EF}=\frac{EB^2}{EF^2}=\frac{BI^2}{FB^2}\) (1)
Ta lại có \(\widehat{FBI}=\widehat{KED},\widehat{BFI}=\widehat{EBI}=\widehat{EKD}\), cho nên \(\Delta FBI~\Delta KED\)
Suy ra \(\frac{BI^2}{FB^2}=\frac{ED^2}{EK^2}=\frac{S_{END}}{S_{EQK}}\) (2) do \(\Delta EDN~\Delta EKQ\)
Từ (1) và (2) ta suy ra \(\frac{S_{END}}{S_{EQK}}=\frac{EI}{EF}.\)