b)

(sin2x + cos2x)cosx + 2cos2x - sinx = 0

⇔ cos2x (cosx + 2) + sinx (2cos2 x – 1) = 0

⇔ cos2x (cosx + 2) + sinx.cos2x = 0

⇔ cos2x (cosx + sinx + 2) = 0

⇔ cos2x  = 0

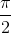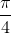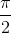⇔ 2x =  + kπ ⇔ x =  + k  (k ∈ )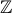

c) 

Đáp án:

x=+ k2

và x= +k2 (k∈Z)

Lời giải:

sin2x-cos2x+3sinx-cosx-1=0

⇔ 2sinxcosx-(1-2sin²x) +3sinx-cosx-1=0

⇔ 2sin²x+2sinxcosx+3sinx-cosx-2=0

⇔ (2sin²x+3sinx-2)+ cosx(2sinx-1)=0

⇔ (2sinx-1)(sinx+2)+cosx(2sinx-1)=0

⇔ (2sinx-1)(sinx+cosx+2)=0

⇔ sinx=

⇔ x=+ k2

hoặc x= +k2 (k∈Z)

(sinx+cosx+2)=0 (vô nghiệm do sinx+cosx+2=sin(x+)+2>0)

6.

\(\Leftrightarrow\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)+\frac{1}{2}sinx.cosx=0\)

\(\Leftrightarrow1-3sin^2x.cos^2x+\frac{1}{2}sinx.cosx=0\)

\(\Leftrightarrow1-\frac{3}{4}sin^22x+\frac{1}{4}sin2x=0\)

\(\Leftrightarrow-3sin^22x+sin2x+4=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sin2x=-1\\sin2x=\frac{4}{3}>1\left(l\right)\end{matrix}\right.\)

\(\Rightarrow2x=-\frac{\pi}{2}+k2\pi\)

\(\Rightarrow x=-\frac{\pi}{4}+k\pi\)

5.

\(\Leftrightarrow\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)=\frac{5}{6}\left[\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x\right]\)

\(\Leftrightarrow1-3sin^2x.cos^2x=\frac{5}{6}\left(1-2sin^2x.cos^2x\right)\)

\(\Leftrightarrow1-\frac{3}{4}sin^22x=\frac{5}{6}\left(1-\frac{1}{2}sin^22x\right)\)

\(\Leftrightarrow\frac{1}{3}sin^22x=\frac{1}{6}\)

\(\Leftrightarrow sin^22x=\frac{1}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}sin2x=\frac{\sqrt{2}}{2}\\sin2x=-\frac{\sqrt{2}}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{8}+k\pi\\x=\frac{3\pi}{8}+k\pi\\x=-\frac{\pi}{8}+k\pi\\x=\frac{5\pi}{8}+k\pi\end{matrix}\right.\)

c.

\(\Leftrightarrow sin\left(3x+\frac{2\pi}{3}\right)=-sin\left(x-\frac{2\pi}{5}-\pi\right)\)

\(\Leftrightarrow sin\left(3x+\frac{2\pi}{3}\right)=sin\left(x-\frac{2\pi}{5}\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}3x+\frac{2\pi}{3}=x-\frac{2\pi}{5}+k2\pi\\3x+\frac{2\pi}{3}=\frac{7\pi}{5}-x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{8\pi}{15}+k\pi\\x=\frac{11\pi}{60}+\frac{k\pi}{2}\end{matrix}\right.\)

d.

\(\Leftrightarrow cos\left(4x+\frac{\pi}{3}\right)=sin\left(\frac{\pi}{4}-x\right)\)

\(\Leftrightarrow cos\left(4x+\frac{\pi}{3}\right)=cos\left(\frac{\pi}{4}+x\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}4x+\frac{\pi}{3}=\frac{\pi}{4}+x+k2\pi\\4x+\frac{\pi}{3}=-\frac{\pi}{4}-x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{36}+\frac{k2\pi}{3}\\x=-\frac{7\pi}{60}+\frac{k2\pi}{5}\end{matrix}\right.\)

a.

\(sin\left(2x+1\right)=-cos\left(3x-1\right)\)

\(\Leftrightarrow sin\left(2x+1\right)=sin\left(3x-1-\frac{\pi}{2}\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}3x-1-\frac{\pi}{2}=2x+1+k2\pi\\3x-1-\frac{\pi}{2}=\pi-2x-1+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+2+k2\pi\\x=\frac{3\pi}{10}+\frac{k2\pi}{5}\end{matrix}\right.\)

b.

\(sin\left(2x-\frac{\pi}{6}\right)=sin\left(\frac{\pi}{4}-x\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{6}=\frac{\pi}{4}-x+k2\pi\\2x-\frac{\pi}{6}=\frac{3\pi}{4}+x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{5\pi}{36}+\frac{k2\pi}{3}\\x=\frac{11\pi}{12}+k2\pi\end{matrix}\right.\)

1, \(\left(sinx+\dfrac{sin3x+cos3x}{1+2sin2x}\right)=\dfrac{3+cos2x}{5}\)

⇔ \(\dfrac{sinx+2sinx.sin2x+sin3x+cos3x}{1+2sin2x}=\dfrac{3+cos2x}{5}\)

⇔ \(\dfrac{sinx+2sinx.sin2x+sin3x+cos3x}{1+2sin2x}=\dfrac{3+cos2x}{5}\)

⇔ \(\dfrac{sinx+cosx-cos3x+sin3x+cos3x}{1+2sin2x}=\dfrac{3+cos2x}{5}\)

⇔ \(\dfrac{sinx+cosx+sin3x}{1+2sin2x}=\dfrac{3+cos2x}{5}\)

⇔ \(\dfrac{2sin2x.cosx+cosx}{1+2sin2x}=\dfrac{3+cos2x}{5}\)

⇔ \(\dfrac{cosx\left(2sin2x+1\right)}{1+2sin2x}=\dfrac{2+2cos^2x}{5}\)

⇒ cosx = \(\dfrac{2+2cos^2x}{5}\)

⇔ 2cos²x - 5cosx + 2 = 0

⇔ \(\left[{}\begin{matrix}cosx=2\\cosx=\dfrac{1}{2}\end{matrix}\right.\)

⇔ \(x=\pm\dfrac{\pi}{3}+k.2\pi\) , k là số nguyên

2, \(48-\dfrac{1}{cos^4x}-\dfrac{2}{sin^2x}.\left(1+cot2x.cotx\right)=0\)

⇔ \(48-\dfrac{1}{cos^4x}-\dfrac{2}{sin^2x}.\dfrac{cos2x.cosx+sin2x.sinx}{sin2x.sinx}=0\)

⇔ \(48-\dfrac{1}{cos^4x}-\dfrac{2}{sin^2x}.\dfrac{cosx}{sin2x.sinx}=0\)

⇔ \(48-\dfrac{1}{cos^4x}-\dfrac{2cosx}{2cosx.sin^4x}=0\)

⇒ \(48-\dfrac{1}{cos^4x}-\dfrac{1}{sin^4x}=0\). ĐKXĐ : sin2x ≠ 0 

⇔ \(\dfrac{1}{cos^4x}+\dfrac{1}{sin^4x}=48\)

⇒ sin⁴x + cos⁴x = 48.sin⁴x . cos⁴x

⇔ (sin²x + cos²x)² - 2sin²x. cos²x = 3 . (2sinx.cosx)⁴

⇔ 1 - \(\dfrac{1}{2}\) . (2sinx . cosx)² = 3(2sinx.cosx)⁴

⇔ 1 - \(\dfrac{1}{2}sin^22x\) = 3sin⁴2x

⇔ \(sin^22x=\dfrac{1}{2}\) (thỏa mãn ĐKXĐ)

⇔ 1 - 2sin²2x = 0

⇔ cos4x = 0

⇔ \(x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\)

3, \(sin^4x+cos^4x+sin\left(3x-\dfrac{\pi}{4}\right).cos\left(x-\dfrac{\pi}{4}\right)-\dfrac{3}{2}=0\)

⇔ \(\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x+\dfrac{1}{2}sin\left(4x-\dfrac{\pi}{2}\right)+\dfrac{1}{2}sin2x-\dfrac{3}{2}=0\)

⇔ \(1-\dfrac{1}{2}sin^22x+\dfrac{1}{2}sin2x-\dfrac{1}{2}cos4x-\dfrac{3}{2}=0\)

⇔ \(\dfrac{1}{2}sin2x-\dfrac{1}{2}cos4x-\dfrac{1}{2}-\dfrac{1}{2}sin^22x=0\)

⇔ sin2x - sin²2x - (1 + cos4x) = 0

⇔ sin2x - sin²2x - 2cos²2x = 0

⇔ sin2x - 2 (cos²2x + sin²2x) + sin²2x = 0

⇔ sin²2x + sin2x - 2 = 0

⇔ \(\left[{}\begin{matrix}sin2x=1\\sin2x=-2\end{matrix}\right.\)

⇔ sin2x = 1

⇔ \(2x=\dfrac{\pi}{2}+k.2\pi\Leftrightarrow x=\dfrac{\pi}{4}+k\pi\)

4, cos5x + cos2x + 2sin3x . sin2x = 0

⇔ cos5x + cos2x + cosx - cos5x = 0

⇔ cos2x + cosx = 0

⇔ \(2cos\dfrac{3x}{2}.cos\dfrac{x}{2}=0\)

⇔ \(cos\dfrac{3x}{2}=0\)

⇔ \(\dfrac{3x}{2}=\dfrac{\pi}{2}+k\pi\)

⇔ x = \(\dfrac{\pi}{3}+k.\dfrac{2\pi}{3}\)

Do x ∈ [0 ; 2π] nên ta có \(0\le\dfrac{\pi}{3}+k\dfrac{2\pi}{3}\le2\pi\)

⇔ \(-\dfrac{1}{2}\le k\le\dfrac{5}{2}\). Do k là số nguyên nên k ∈ {0 ; 1 ; 2}

Vậy các nghiệm thỏa mãn là các phần tử của tập hợp 

\(S=\left\{\dfrac{\pi}{3};\pi;\dfrac{5\pi}{3}\right\}\)

a)      

\(\begin{array}{l}\sin \left( {2x - \frac{\pi }{6}} \right) =  - \frac{{\sqrt 3 }}{2}\\ \Leftrightarrow \sin \left( {2x - \frac{\pi }{6}} \right) = \sin \left( { - \frac{\pi }{3}} \right)\end{array}\)

\(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}2x - \frac{\pi }{6} =  - \frac{\pi }{3} + k2\pi \\2x - \frac{\pi }{6} = \pi  + \frac{\pi }{3} + k2\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}2x =  - \frac{\pi }{6} + k2\pi \\2x = \frac{{3\pi }}{2} + k2\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x =  - \frac{\pi }{{12}} + k\pi \\x = \frac{{3\pi }}{4} + k\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\)

b)     \(\begin{array}{l}\cos \left( {\frac{{3x}}{2} + \frac{\pi }{4}} \right) = \frac{1}{2}\\ \Leftrightarrow \cos \left( {\frac{{3x}}{2} + \frac{\pi }{4}} \right) = \cos \frac{\pi }{3}\end{array}\)

\(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}\frac{{3x}}{2} + \frac{\pi }{4} = \frac{\pi }{3} + k2\pi \\\frac{{3x}}{2} + \frac{\pi }{4} = \frac{{ - \pi }}{3} + k2\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{18}} + \frac{{k4\pi }}{3}\\x = \frac{{ - 7\pi }}{{18}} + \frac{{k4\pi }}{3}\end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\)

c)       

\(\begin{array}{l}\sin 3x - \cos 5x = 0\\ \Leftrightarrow \sin 3x = \cos 5x\\ \Leftrightarrow \cos 5x = \cos \left( {\frac{\pi }{2} - 3x} \right)\\ \Leftrightarrow \left[ \begin{array}{l}5x = \frac{\pi }{2} - 3x + k2\pi \\5x =  - \left( {\frac{\pi }{2} - 3x} \right) + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}8x = \frac{\pi }{2} + k2\pi \\2x =  - \frac{\pi }{2} + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{16}} + \frac{{k\pi }}{4}\\x =  - \frac{\pi }{4} + k\pi \end{array} \right.\end{array}\)

d)      

\(\begin{array}{l}{\cos ^2}x = \frac{1}{4}\\ \Leftrightarrow \left[ \begin{array}{l}\cos x = \frac{1}{2}\\\cos x =  - \frac{1}{2}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\cos x = \cos \frac{\pi }{3}\\\cos x = \cos \frac{{2\pi }}{3}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi \\x =  - \frac{\pi }{3} + k2\pi \end{array} \right.\\\left[ \begin{array}{l}x = \frac{{2\pi }}{3} + k2\pi \\x =  - \frac{{2\pi }}{3} + k2\pi \end{array} \right.\end{array} \right.\end{array}\)

e)      

\(\begin{array}{l}\sin x - \sqrt 3 \cos x = 0\\ \Leftrightarrow \frac{1}{2}\sin x - \frac{{\sqrt 3 }}{2}\cos x = 0\\ \Leftrightarrow \cos \frac{\pi }{3}.\sin x - \sin \frac{\pi }{3}.\cos x = 0\\ \Leftrightarrow \sin \left( {x - \frac{\pi }{3}} \right) = 0\\ \Leftrightarrow \sin \left( {x - \frac{\pi }{3}} \right) = \sin 0\\ \Leftrightarrow x - \frac{\pi }{3} = k\pi ;k \in Z\\ \Leftrightarrow x = \frac{\pi }{3} + k\pi ;k \in Z\end{array}\)

f)       

\(\begin{array}{l}\sin x + \cos x = 0\\ \Leftrightarrow \frac{{\sqrt 2 }}{2}\sin x + \frac{{\sqrt 2 }}{2}\cos x = 0\\ \Leftrightarrow \cos \frac{\pi }{4}.\sin x + \sin \frac{\pi }{4}.\cos x = 0\\ \Leftrightarrow \sin \left( {x + \frac{\pi }{4}} \right) = 0\\ \Leftrightarrow \sin \left( {x + \frac{\pi }{4}} \right) = \sin 0\\ \Leftrightarrow x + \frac{\pi }{4} = k\pi ;k \in Z\\ \Leftrightarrow x =  - \frac{\pi }{4} + k\pi ;k \in Z\end{array}\)

Câu 2 bạn coi lại đề

3.

\(1+2sinx.cosx-2cosx+\sqrt{2}sinx+2cosx\left(1-cosx\right)=0\)

\(\Leftrightarrow sin2x-\left(2cos^2x-1\right)+\sqrt{2}sinx=0\)

\(\Leftrightarrow sin2x-cos2x=-\sqrt{2}sinx\)

\(\Leftrightarrow\sqrt{2}sin\left(2x-\frac{\pi}{4}\right)=\sqrt{2}sin\left(-x\right)\)

\(\Leftrightarrow sin\left(2x-\frac{\pi}{4}\right)=sin\left(-x\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{4}=-x+k2\pi\\2x-\frac{\pi}{4}=\pi+x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow...\)

4.

Bạn coi lại đề, xuất hiện 2 số hạng \(cos4x\) ở vế trái nên chắc là bạn ghi nhầm

5.

\(\Leftrightarrow sinx.sin2x-cosx.sin^22x=2cos^2\left(\frac{\pi}{4}-x\right)-1\)

\(\Leftrightarrow sinx.sin2x-cosx.sin^22x=cos\left(\frac{\pi}{2}-2x\right)\)

\(\Leftrightarrow sinx.sin2x-cosx.sin^22x=sin2x\)

\(\Leftrightarrow sin2x\left(sinx-cosx.sin2x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sin2x=0\Leftrightarrow x=...\\sinx-cosx.sin2x-1=0\left(1\right)\end{matrix}\right.\)

Xét (1):

\(\Leftrightarrow sinx-1-2sinx.cos^2x=0\)

\(\Leftrightarrow sinx-1-2sinx\left(1-sin^2x\right)=0\)

\(\Leftrightarrow2sin^3x-sinx-1=0\)

\(\Leftrightarrow\left(sinx-1\right)\left(2sin^2x+2sinx+1\right)=0\)

\(\Leftrightarrow...\)

ĐK: \(x\ne k\pi\)

\(\dfrac{1+sin2x+cos2x}{1+cot^2x}=sinx.\left(sin2x+2sin^2x\right)\)

\(\Leftrightarrow\dfrac{1+sin2x+cos2x}{\dfrac{cos^2x+sin^2x}{sin^2x}}=sinx.\left(2sinx.cosx+2sin^2x\right)\)

\(\Leftrightarrow\dfrac{1+sin2x+cos2x}{\dfrac{1}{sin^2x}}=2sin^2x.\left(cosx+sinx\right)\)

\(\Leftrightarrow1+sin2x+cos2x=2cosx+2sinx\)

\(\Leftrightarrow1+2sinx.cosx+2cos^2x-1=2cosx+2sinx\)

\(\Leftrightarrow\left(cosx-1\right).\left(sinx+cosx\right)=0\)

\(\Leftrightarrow\left(cosx-1\right).sin\left(x+\dfrac{\pi}{4}\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\sin\left(x+\dfrac{\pi}{4}\right)=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x+\dfrac{\pi}{4}=k\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=-\dfrac{\pi}{4}+k\pi\end{matrix}\right.\)

Cảm ơn bạn nhé

1a.

Đặt \(5x+6=u\)

\(cos2u+4\sqrt{2}sinu-4=0\)

\(\Leftrightarrow1-2sin^2u+4\sqrt{2}sinu-4=0\)

\(\Leftrightarrow2sin^2u-4\sqrt{2}sinu+3=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sinu=\dfrac{3\sqrt{2}}{2}>1\left(loại\right)\\sinu=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)

\(\Rightarrow sin\left(5x+6\right)=\dfrac{\sqrt{2}}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}5x+6=\dfrac{\pi}{4}+k2\pi\\5x+6=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{6}{5}+\dfrac{\pi}{20}+\dfrac{k2\pi}{5}\\x=-\dfrac{6}{5}+\dfrac{3\pi}{20}+\dfrac{k2\pi}{5}\end{matrix}\right.\)

1b.

Đặt \(2x+1=u\)

\(cos2u+3sinu=2\)

\(\Leftrightarrow1-2sin^2u+3sinu=2\)

\(\Leftrightarrow2sin^2u-3sinu+1=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sinu=1\\sinu=\dfrac{1}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}sin\left(2x+1\right)=1\\sin\left(2x+1\right)=\dfrac{1}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+1=\dfrac{\pi}{2}+k2\pi\\2x+1=\dfrac{\pi}{6}+k2\pi\\2x+1=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}+\dfrac{\pi}{4}+k\pi\\x=-\dfrac{1}{2}+\dfrac{\pi}{12}+k\pi\\x=-\dfrac{1}{2}+\dfrac{5\pi}{12}+k\pi\end{matrix}\right.\)

\(\left(2cosx+\sqrt{3}\right)\left(cos2x+2sinx-\sqrt{3}\right)=1-4\left(1-cos^2x\right)\)

\(\Leftrightarrow\left(2cosx+\sqrt{3}\right)\left(cos2x+2sinx-\sqrt{3}\right)=4cos^2x-3\)

\(\Leftrightarrow\left(2cosx+\sqrt{3}\right)\left(cos2x+2sinx-\sqrt{3}\right)=\left(2cosx+\sqrt{3}\right)\left(2cosx-\sqrt{3}\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}cosx=-\dfrac{\sqrt{3}}{2}\Rightarrow x=...\\cos2x+2sinx-\sqrt{3}=2cosx-\sqrt{3}\left(1\right)\end{matrix}\right.\)

\(\left(1\right)\Leftrightarrow cos^2x-sin^2x-2\left(cosx-sinx\right)=0\)

\(\Leftrightarrow\left(cosx-sinx\right)\left(cosx+sinx\right)-2\left(cosx-sinx\right)=0\)

\(\Leftrightarrow\left(cosx-sinx\right)\left(cosx+sinx-2\right)=0\)

\(\Leftrightarrow...\)