Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Xác định xem hai lực đó là lực đồng quy hay hai lực song song, cùng chiều.
- Sử dụng các bộ dụng cụ thí nghiệm thích hợp.


-Tàu sẽ chuyển động theo hướng tổng hợp lực \(\overrightarrow{F}\).
-Để tính được độ lớn của lực kéo tác dụng lên tàu ta cần xác định lực \(F_1,F_2\) và góc tạo bởi hai lực đó.


Bài 1:
\(\alpha= 0\) \(\Rightarrow F = F_1+F_2 = 16+12=28N\)
\(\alpha = 30^0\)\(\Rightarrow F^2=16^2+12^2+2.16.12.\cos30^0=...\Rightarrow F\)
Các trường hợp khác bạn tự tính nhé.
Bài 2:
Ta có: \(F_1=k.\Delta \ell_1=k.(0,24-0,12)=0,12.k=5\) (1)
\(F_1=k.\Delta \ell_2=k.(\ell-0,12)=10\) (2)
Lấy (2) chia (1) vế với vế: \(\dfrac{\ell-0,12}{0,12}=2\)
\(\Rightarrow \ell = 0,36m = 36cm\)
Bài 3:
Áp lực lên sàn: \(N=P=mg\)
Áp dụng định luật II Niu tơn ta có: \(F=m.a\Rightarrow -F_{ms}=ma\)
\(\Rightarrow a = \dfrac{-F_{ms}}{m}= \dfrac{-\mu.N}{m}== \dfrac{-\mu.mg}{m}=-\mu .g =- 0,1.10=-1\)(m/s2)
Quãng đường vật đi được đến khi dừng lại là \(S\)
Áp dụng công thức độc lập: \(v^2-v_0^2=2.a.S\)
\(\Rightarrow 0^2-10^2=2.1.S\Rightarrow S = 50m\)

1.
Cách để \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) đồng quy: Di chuyển hai lực kế sao cho dây cao su và các đoạn dây chỉ song song với mặt phẳng và tâm O của thước trùng với giao điểm của sợi dây và dây cao su.
2.
Các xác định lực thay thế hai lực thành phần:
+ Đánh dấu lên bảng sắt điểm A của đầu dây cao su
+ Tháo một lực kế ra
+ Di chuyển lực kế còn lại sao cho đầu dây cao su trùng với điểm A đã đánh dấu
3.
Sau khi bố trí thí nghiệm như ở câu 2 thì ta ghi lại đáp án của lực kế, đó là số chỉ của lực tổng hợp, thực hiện thí nghiệm thêm ít nhất 2 lần.

Nếu F1=F2
do góc giữa vecto F1, F2=60o
áp dụng định lý hàm cos
F2=F12+ F22+2F1F2cos (vecto)
=> F1=0,58F
|
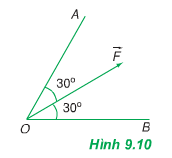
Phân tích lực F→ thành hai lực F1−→ và F2−→ theo hai phương OA và OB (hình 9.10). Giá trị nào sau đây là độ lớn của hai lực thành phần? A. F1 = F2 = F; B. F1 = F2 = 12F; C. F1 = F2 = 1,15F; D. F1 = F2 = 0,58F. |

1.
Ta thấy: \({10^2} = \sqrt {{6^2} + {8^2}} \Rightarrow {F^2} = \sqrt {F_1^2 + F_2^2} \)
Suy ra \({F_1} \bot {F_2}\)
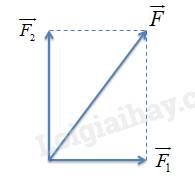
2.
a)
Biểu diễn các lực kéo của mỗi tàu và hợp lực tác dụng vào tàu chở hàng:
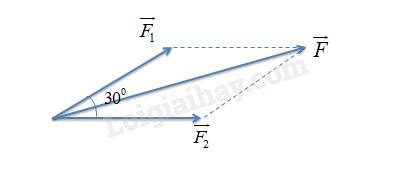
b)
Độ lớn của hợp lực là:
\(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}\cos \left( {{F_1},{F_2}} \right)} \)
\( \Leftrightarrow F = \sqrt {{{8000}^2} + {{8000}^2} + 2.8000.8000.\cos {{30}^0}} \)
\( \Leftrightarrow F = 15455\left( N \right)\)
c)
Hợp lực có:
- Chiều: hướng về phía trước
- Phương: hợp với \(\overrightarrow {{F_1}} \) góc \({15^0}\)
d) Nếu góc giữa hai dây cáp bằng \({90^0}\) thì hợp lực có:
- Phương: xiên
- Chiều hướng sang trái hoặc phải.
- Độ lớn: \(F = \sqrt {F_1^2 + F_2^2} \)



1.
- Lắp các dụng cụ như hình vẽ
- Dùng bút dạ đánh dấu vị trí thanh và vị trí A, B lên bảng thép
- Tháo các quả nặng và móc tất cả quả nặng đã dùng vào một móc treo trên thanh kim loại
- Điều chỉnh con trượt sao cho vị trí của thanh kim loại trùng với vị trí ban đầu được đánh dấu.
2.
Để F1 và F2 song song thì treo các quả cân thỏa mãn biểu thức:
\(\frac{{{F_1}}}{{{F_2}}} = \frac{{{d_2}}}{{{d_1}}}\)
3.
Cách xác định lực tổng hợp hai hai lực thành phần:
- Xác định vị trí lực thay thế hai lực thành phần giống câu 1
- Tính độ lớn của lực đó