
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn vào trang Wolfram Alpha sẽ thấy:
20182017 có 6667 chữ số
20172018 có 6669 chữ số
Vậy 20182017 < 20172018
*189* chia hết cho cả 3 và 5
*47* chia hết cho cả 2,3,5,9
Các bạn ghi lời giải giúp mk nhé! Mk sẽ kick

*189* chia hết cho cả 3 và 5
=> Ta có hai trường hợp là * ở cuối là 0 hoặc là 5
Nếu là 0 thì: 1+8+9+0=18
=> Ta có: * ở đầu là các số 3;6;9 ( bò 0 vì hàng đầu không thể nào là 0)
Nếu là 5 thì: 1+8+9+5=23
=>* ở đầu là 1;4;7
Vậy ta có các trường hợp sau:
- Số đó là: 31890
hoặc: 61890
hoặc: 91890
hoặc: 11895
hoặc 41895
hoặc 71895
Theo bài ra , ta có :
*189* chia hết cho cả 3 và 5
=> Ta có hai trường hợp là * ở cuối là 0 hoặc là 5
Nếu là 0 thì: 1+8+9+0=18
=> Ta có: * ở đầu là các số 3;6;9 ( bò 0 vì hàng đầu không thể nào là 0)
Nếu là 5 thì: 1+8+9+5=23
=>* ở đầu là 1;4;7
Vậy ta có các trường hợp sau:
- Số đó là: 31890
hoặc: 61890
hoặc: 91890
hoặc: 11895
hoặc 41895
hoặc 71895

Bài 3:
Gọi số học sinh là x
Theo đề, ta có: \(x-5\in BC\left(8;12;15\right)\)
mà 300<=x<=400
nên x=365

\(a\)có dạng \(6k+1\)hoặc \(6k-1\).
Với \(a=6k+1\):
\(A=4\left(6k+1\right)^2+3\left(6k+1\right)+5\equiv4+3+5\equiv0\left(mod6\right)\).
Với \(a=6k-1\):
\(A=4\left(6k-1\right)^2+3\left(6k-1\right)+5\equiv4-3+5\equiv0\left(mod6\right)\).

⇒ (x + 1)2 = 16 = (\(\pm4\))2
⇒ \(\left[{}\begin{matrix}x+1=4\\x+1=-4\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=3\\x=-5\end{matrix}\right.\)

Gọi số cần tìm là ab
Để số ab chia cho 5 dư 3 thì
b = 3 hoặc 8
Vì số ab chia hết cho 2
=> b \(\ne\)3 mà b = 8
Và số ab có các chữ số giống nhau => số đó là 88
Vậy số cần tìm là 88

\(\left(x-3\right)\left(x^2+5\right)=0\)
\(\Rightarrow x-3=0\) hoặc \(x^2+5=0\)
x= 3 \(x^2=-5\) ( vô lý- do \(x^2\ge0\) với mọi x)
Vậy ...

\(\Rightarrow5^2\cdot5^{x+3}=5^6\\ \Rightarrow5^{x+3}=5^4\\ \Rightarrow x+3=4\\ \Rightarrow x=1\)

ab+bc+ca=abc
a \(\times\)10 + b + b\(\times\)10 + c + c \(\times\)10 + a = a \(\times\)100 + b\(\times\)10 + c
a\(\times\)11 + b \(\times\)11 + c\(\times\)11 = a \(\times\)100 + b\(\times\)10 + c
b + c \(\times\)10 = a\(\times\)89
a chỉ có thể bằng 1 nếu a = 2 hoặc lớn hơn 2 thì cho dù b và c lớn nhất là 9 thì
9 + 9 \(\times\)10 = 99 mà 2 \(\times\)89 = 178
=> a = 1
b + c \(\times\)10 = 1\(\times\)89 = 89
=> c = 8
=> b = 9
vậy a = 1
b = 9
c = 8
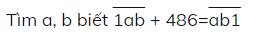

Ta có: \(\overline{1ab}=100+\overline{ab}\)
Và: \(\overline{ab1}=10\overline{ab}+1\)
\(\Rightarrow100+\overline{ab}+486=10\overline{ab}+1\)
\(\Rightarrow\overline{ab}-10\overline{ab}=1-100-486\)
\(\Rightarrow-9\overline{ab}=-585\)
\(\Rightarrow\overline{ab}=\dfrac{-585}{-9}=65\)