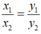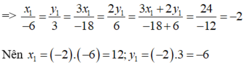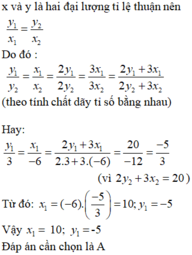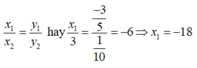Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Giả sử $y$ tỉ lệ thuận với $x$ theo hệ số tỉ lệ $k$. Khi đó $y=kx$
$y_2=kx_2$
$\Rightarrow k=\frac{y_2}{x_2}=\frac{3}{-4}$
$y_1=kx_1$
$y_1-3x_1=-7$
$kx_1-3x_1=-7$
$x_1(k-3)=-7$. Thay $k=\frac{3}{-4}$ thì:
$x_1=\frac{-7}{k-3}=\frac{-7}{\frac{3}{-4}-3}=\frac{28}{15}$
$y_1=kx_1=\frac{3}{-4}.\frac{28}{15}=\frac{-7}{5}$

Suy ra x 1 − 4 = y 1 3 = y 1 − x 1 3 − ( − 4 ) = − 7 7 = − 1
Nên x 1 = ( − 1 ) . ( − 4 ) = 4 ; y 1 = ( − 1 ) .3 = − 3
Đáp án cần chọn là D

Lời giải:
Vì $x,y$ là 2 đại lượng tỉ lệ thuận nên đặt $y=ax$.
Ta có:
$y_2=ax_2$
$3=a(-4)\Rightarrow a=\frac{-3}{4}$. Vậy $y=\frac{-3}{4}x$. Thay vào điều kiện $y_1-x_1=7$ ta có:
$\frac{-3}{4}x_1-x_1=7$
$\frac{-7}{4}x_1=7$
$\Rightarrow x_1=-4$
$y_1=7+x_1=7+(-4)=3$
Đáp án C

a: x và y là hai đại lượng tỉ lệ thuận
nên \(\dfrac{x_1}{x_2}=\dfrac{y_1}{y_2}\)
=>\(\dfrac{x_1}{2}=\dfrac{-3}{4}:\dfrac{1}{7}=-\dfrac{3}{4}\cdot7=-\dfrac{21}{4}\)
=>\(x_1=-\dfrac{21}{4}\cdot2=-\dfrac{21}{2}\)
b: \(\dfrac{x_1}{x_2}=\dfrac{y_1}{y_2}\)
=>\(\dfrac{x_1}{-4}=\dfrac{y_1}{3}\)
mà \(y_1-x_1=-2\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x_1}{-4}=\dfrac{y_1}{3}=\dfrac{y_1-x_1}{3-\left(-4\right)}=-\dfrac{2}{7}\)
=>\(x_1=\dfrac{-2}{7}\cdot\left(-4\right)=\dfrac{8}{7};y_1=\dfrac{-2}{7}\cdot3=-\dfrac{6}{7}\)