Có x < y => \(\frac{a}{m}\) < \(\frac{b}{m}\) => a < b (vì m > 0)

x = \(\frac{a}{m}\) = \(\frac{2a}{2m}\) - \(\frac{a+a}{2m}\) < \(\frac{a+b}{2m}\) = z

=> x < z (1)

y = \(\frac{b}{m}\) = \(\frac{2b}{2m}\) = \(\frac{b+b}{2m}\) > \(\frac{a+b}{2m}\) (b > a)

=> y > z (2)

Từ (1) và (2) suy ra x < z < y.

Theo đề bài ta có x = a/m, y = b/m (a, b, m ∈ Z, b # 0)
Vì x < y nên ta suy ra a < b
Ta có: x = 2a/2m, y = 2b/2m; z = (a+b)/2m
Vì a < b => a + a < a + b => 2a < a + b
Do 2a < a + b nên x < z (1)
Vì a < b => a + b < b + b => a + b < 2b
Do a + b < 2b nên z < y (2)
Từ (1) và (2) ta suy ra x < z < y

Vì x < y (a/m < b/m) và m > 0 nên a < b . 

x = a / m = 2a / 2m ; y = b / m = 2b / 2m ; z = a + b / 2m

a < b => a + a < a + b < b + b <=> 2a < a + b < 2b => 2a / 2m < a + b / 2m < 2b / 2m => x < z < y

ta có x=a/m = 2a/2m ; y= b/m= 2b/2m ; z= (a+b)/2m
lại có x<y <=> a<b (do m>0)
<=> a+a < a+b < b + b 
<=> 2a < a+b < 2b 
<=> 2a/2m <(a+b)/2m <2b/2m
<=> x<z<y

 x =a/m =>. x = 2a/2m 
y =b/m => y = 2b/2m 
z = (a+b)/2m 
theo giả thiết a < b => a + b < b + b => a + b < 2b ........(1) 
Ngòa i ra, a < b => a + a < a + b => 2a < a + b ........(2) 
Suy ra: 
2a < a +b < 2b 
Suy ra (chia 2 vế cho 2m) : 
2a/2m < (a +b)/2m < 2b 
R út gọn ta được : x < z <y

ta có : x < y hay a/m < b/m   => a < b.

So sánh x, y, z ta chuyển chúng cùng mẫu : 2m

x =  a/m  = 2a/ 2m và y = b/m = 2b/2m  và z = (a + b) / 2m

mà : a < b

suy ra : a + a < b + a

hay 2a < a + b

suy ra x < z (1)

mà : a < b

suy ra : a + b < b + b

hay a + b < 2b

suy ra z < y (2)

Với a, b ∈ Z, b> 0

- Khi a , b cùng dấu thì \(\frac{a}{b}\)> 0

- Khi a,b khác dấu thì \(\frac{a}{b}\)< 0

Tổng quát: Số hữu tỉ  \(\frac{a}{b}\) ( a,b ∈ Z, b # 0) dương nếu a,b cùng dấu, âm nếu a, b khác dấu, bằng 0 nếu a = 0

Theo đề bài ta có x = a/m, y = b/m (a, b, m ∈ Z, b # 0)
Vì x < y nên ta suy ra a < b
Ta có: x = 2a/2m, y = 2b/2m; z = (a+b)/2m
Vì a < b => a + a < a + b => 2a < a + b
Do 2a < a + b nên x < z (1)
Vì a < b => a + b < b + b => a + b < 2b
Do a + b < 2b nên z < y (2)
Từ (1) và (2) ta suy ra x < z < y

Theo đề bài ta có 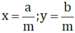 (a, b, m ∈ Z; m > 0).

Quy đồng mẫu số các phân số ta được: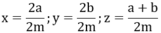 

Nhận xét: mẫu số 2m > 0 nên để so sánh x, y, z ta so sánh các tử số 2a, 2b, a+b.

   Vì a < b nên a + a < b + a hay 2a < a + b.

   Vì a < b nên a + b < b + b hay a + b < 2b.

Vậy ta có 2a < a+b < 2b nên 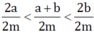 hay x < z < y.

Tham khảo câu hỏi : Câu hỏi của Thiên Thiên - Toán lớp 7 | Học trực tuyến