
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A=\(25x^2+3y^2-10x+11=\)\(\left(5x\right)^2-2.5.x+1^2+3y^2+10=\)\(\left(5x+1\right)^2+3y^2+10\ge10\)
(Vì\(\left(5x+1\right)^2\ge0\forall x\),\(3y^2\ge0\forall y\))
Dấu "=" xảy ra \(\Leftrightarrow x=\frac{-1}{5},y=0\)
Vậy A max=10\(\Leftrightarrow x=\frac{-1}{5},y=0\)

\(B=25x^2+3y^2-10y+11\)
\(=25x^2+3\left(y^2-\frac{10}{3}y+\frac{11}{3}\right)\)
\(=25x^2+3\left(y^2-2.y.\frac{5}{3}+\frac{25}{9}+\frac{8}{9}\right)\)
\(=25x^2+3\left(y-\frac{5}{3}\right)^2+\frac{8}{3}\ge\frac{8}{3}\)
Đẳng thức xảy ra khi x = 0; y = 5/3
Vậy...

A=25x2+3y^2-10x+11
A=25x^2+3y^2-10x+1+10
A=(25x^2-10x+1)+3y^2+10
A=(5x-1)2+3y2+10
Vì (5x-1)2 > hoặc = 0 với mọi x thuộc Z
Vì 3,y^2 luôn > hoặc = 0 với mọi x thuộc Z => 3y2 luôn > hoặc = 0 với mọi x thuộc Z
=> (5x-1)2+3y2> hoặc bằng o với mọi x thuộc Z
=> (5x-1)2+3y2+10 luôn lớn hơn hoặc bằng 10 với mọi x thuộc Z
A luôn lớn hơn hoặc bằng 10 với mọi x thuộc Z
=> Amin=10
Dấu "=" xảy ra <=> (5x-1)2+3y2=0
=> 5x-1=0
=> 3y2=0
=> x=\(\frac{1}{5}\)
=> y=0
KL Amin=10 <=> x=\(\frac{1}{5}\);y=0


Câu 2:
a: ĐKXĐ: \(x\notin\left\{0;2\right\}\)
b: Sửa đề: \(A=\left(\dfrac{2x-x^2}{2x^2+8}-\dfrac{2x^2}{x^3-2x^2+4x-8}\right)\cdot\left(\dfrac{2}{x^2}-\dfrac{x-1}{x}\right)\)
\(=\left(\dfrac{2x-x^2}{2\left(x^2+4\right)}-\dfrac{2x^2}{\left(x-2\right)\left(x^2+4\right)}\right)\cdot\dfrac{2-x\left(x-1\right)}{x^2}\)
\(=\left(\dfrac{\left(2x-x^2\right)\left(x-2\right)-4x^2}{2\left(x^2+4\right)\left(x-2\right)}\right)\cdot\dfrac{2-x^2+x}{x^2}\)
\(=\dfrac{\left(x^2-2x\right)\left(x-2\right)+4x^2}{2\left(x^2+4\right)\left(x-2\right)}\cdot\dfrac{x^2-x-2}{x^2}\)
\(=\dfrac{x^3-2x^2-2x^2+4x+4x^2}{2\left(x^2+4\right)\left(x-2\right)}\cdot\dfrac{\left(x-2\right)\left(x+1\right)}{x^2}\)
\(=\dfrac{x^3+4x}{2\left(x^2+4\right)}\cdot\dfrac{x+1}{x^2}\)
\(=\dfrac{x\left(x^2+4\right)\left(x+1\right)}{2\left(x^2+4\right)\cdot x^2}=\dfrac{x+1}{2x}\)
c: Khi x=2024 thì \(A=\dfrac{2024+1}{2\cdot2024}=\dfrac{2025}{4048}\)
Câu 1:
a: \(25x^2\left(x-3y\right)-15\left(3y-x\right)\)
\(=25x^2\left(x-3y\right)+15\left(x-3y\right)\)
\(=\left(x-3y\right)\left(25x^2+15\right)\)
\(=\left(x-3y\right)\cdot5\cdot\left(5x^2+3\right)\)
b: \(x^4-5x^2+4\)
\(=x^4-x^2-4x^2+4\)
\(=\left(x^4-x^2\right)-\left(4x^2-4\right)\)
\(=x^2\left(x^2-1\right)-4\left(x^2-1\right)\)
\(=\left(x^2-1\right)\left(x^2-4\right)=\left(x-1\right)\left(x+1\right)\left(x-2\right)\left(x+2\right)\)

\(\frac{3y^2}{-25x^2+20xy-5y^2}\)=\(\frac{3y^2}{-\left(25x^2-2\cdot5x\cdot2y+4y^2\right)-y^2}\)=\(\frac{3y^2}{-\left(5x-2y\right)^2-y^2}\)với x; y ko đồng thời bằng 0
Do \(\text{-(5x-2y)}^2\) \(\le\)0 với mọi x;y \(\Rightarrow\)-(5x-2y)\(^2\)-y\(^2\)\(\le\)-y\(^2\)\(\Rightarrow\)\(\frac{3y^2}{-\left(5x-2y\right)^2-y^2}\)\(\ge\)-3
Đẳng thức xảy ra\(\leftrightarrow\)5x=2y và x\(\ne\)0;y\(\ne\)0
thank bạn nhiều nha vậy là do mình tách sai rồi mình lại để x ra ngoài ở mẫu chứ ko phải y nên ko ra là 5x=2y thank nhiều nhé

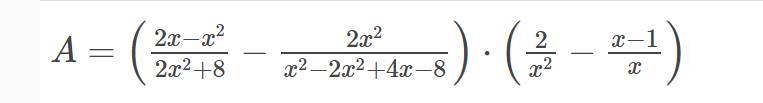
TL
3y2+3y+25x2-10x+4
HT
TL:
3y2 + 3y + 25x2 - 10x + 4
~HT~