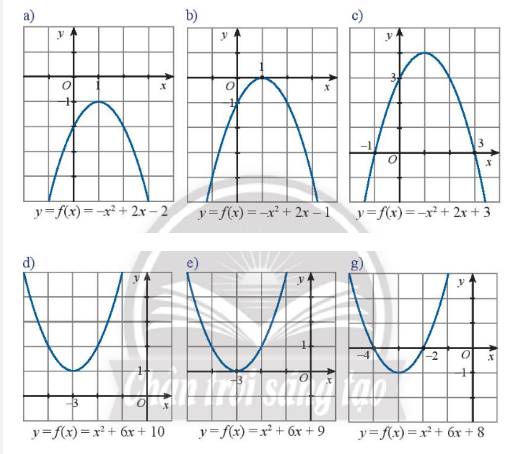
a) Dựa vào đồ thị ta thấy hàm số đã cho vô nghiệm

          Biệt thức \(\Delta  = {2^2} - 4.\left( { - 1} \right).\left( { - 2} \right) =  - 4 < 0\)

          Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)

          Đồ thị nằm dưới trục hoành với mọi x

Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với \(\forall x \in \mathbb{R}\)

b) Dựa vào đồ thị ta thấy hàm số đã cho có nghiệm kép \({x_1} = {x_2} = 1\)

Biệt thức \(\Delta  = {2^2} - 4.\left( { - 1} \right).\left( { - 1} \right) = 0\)

          Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)

          Đồ thị nằm dưới trục hoành với mọi x

Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với \(\forall x \in \mathbb{R}\)

c) Dựa vào đồ thị ta thấy hàm số đã cho có hai nghiệm phân biệt  \({x_1} =  - 1;{x_2} = 3\)

Biệt thức \(\Delta  = {2^2} - 4.\left( { - 1} \right).3 = 16 > 0\)

          Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)

Đồ thị nằm dưới trục hoành khi  \(x \in \left( { - \infty , - 1} \right) \cup \left( {3, + \infty } \right)\)

Đồ thị nằm trên trục hoành với mọi \(x \in \left( { - 1,3} \right)\)

Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) khi \(x \in \left( { - \infty , - 1} \right) \cup \left( {3, + \infty } \right)\)

d) Dựa vào đồ thị ta thấy hàm số bậc hai đã cho vô nghiệm

Biệt thức \(\Delta  = {6^2} - 4.1.10 =  - 4 < 0\)

          Ta thấy hệ số của \({x^2}\) là \(1 > 0\)

Đồ thị nằm trên trục hoành với mọi \(x\)

Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với mọi \(x \in \mathbb{R}\)

e) Dựa vào đồ thị ta thấy hàm số đã cho có nghiệm kép \({x_1} = {x_2} =  - 3\)

Biệt thức \(\Delta  = {6^2} - 4.1.9 = 0\)

          Ta thấy hệ số của \({x^2}\) là \(1 > 0\)

          Đồ thị nằm trên trục hoành với mọi x

Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với mọi \(x \in \mathbb{R}\)

g) ) Dựa vào đồ thị ta thấy hàm số đã cho có hai nghiệm phân biệt  \({x_1} =  - 4;{x_2} =  - 2\)

Biệt thức \(\Delta  = {6^2} - 4.1.8 = 4 > 0\)

          Ta thấy hệ số của \({x^2}\) là \(1 > 0\)

Đồ thị nằm trên trục hoành khi  \(x \in \left( { - \infty , - 4} \right) \cup \left( { - 2, + \infty } \right)\)

Đồ thị nằm dưới trục hoành với mọi \(x \in \left( { - 4, - 2} \right)\)

Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) khi \(x \in \left( { - \infty , - 4} \right) \cup \left( { - 2, + \infty } \right)\)

Bước 1: Vẽ đường thẳng \(d_1: y-2x=2\) đi qua (0;2) và (-1;0). 

Lấy điểm O(0;0) không thuộc \(d_1\). Vì 0-2.0=0<2 nên O thuộc miền nghiệm

Miền nghiệm của BPT \(y - 2x \le 2\) là nửa mp bờ \(d_1\), chứa điểm O.

Bước 2: Vẽ đường thẳng \(d_2: y=4\) đi qua (0;4) và (1;4). 

Lấy điểm O(0;0) không thuộc \(d_2\). Vì 0<4 nên O thuộc miền nghiệm.

Miền nghiệm của BPT \(y \le 4\) là nửa mp bờ \(d_2\), chứa điểm O.

Bước 3: Vẽ đường thẳng \(d_3: x=5\) đi qua (5;0) và (5;1). 

Lấy điểm O(0;0) không thuộc \(d_3\). Vì 0<5 nên O thuộc miền nghiệm

Miền nghiệm của BPT \(x \le 5\) là nửa mp bờ \(d_3\), chứa điểm O.

Bước 4: Vẽ đường thẳng \(d_4: x + y = - 1\) đi qua (-1;0) và (0;-1). 

Lấy điểm O(0;0) không thuộc \(d_4\). Vì 0+0=0>-1 nên O thuộc miền nghiệm.

Miền nghiệm của BPT \(x + y \ge  - 1\) là nửa mp bờ \(d_4\), chứa điểm O.

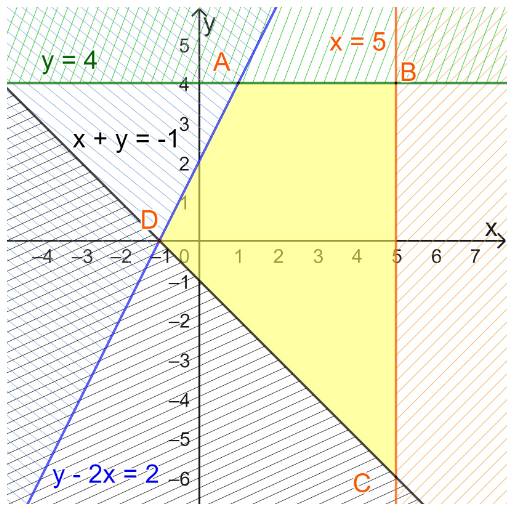
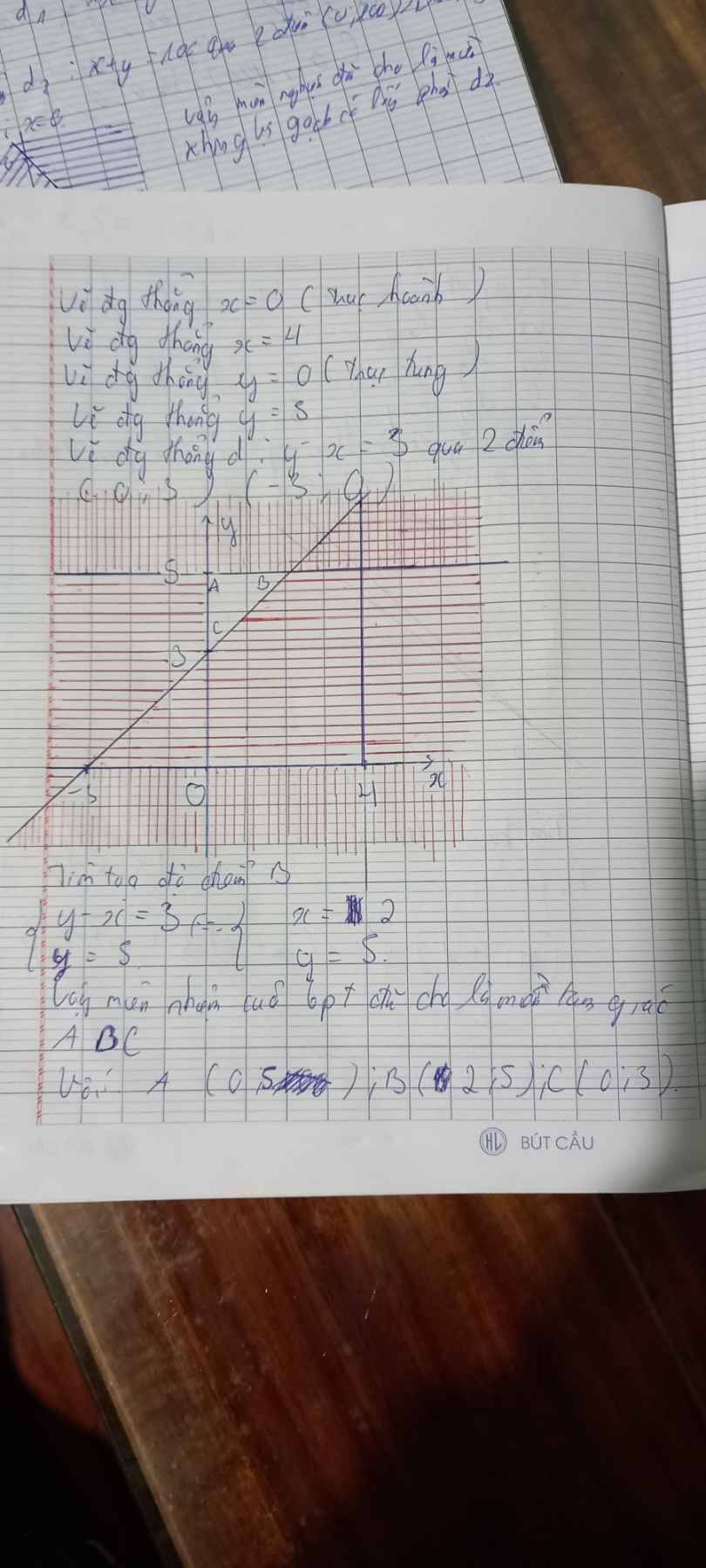
Miền biểu diễn nghiệm của hệ bất phương trình là miền tứ giác ABCD với

A(1;4); B(5;4), C(5;-6); D(-1;0).

Giá trị F tại các điểm A, B, C, D lần lượt là:

\(F\left( {1;4} \right) =  - 1 - 4 =  - 5\)

\(F\left( {5;4} \right) =  - 5 - 4 =  - 9\)

\(F\left( {5;-6} \right) =  - 5 - (-6) =  1\)

\(F\left( { - 1;0} \right) =  - \left( { - 1} \right) - 0 = 1\)

Vậy giá trị lớn nhất của biểu thức F(x;y) là 1 và giá trị nhỏ nhất của biểu thức F(x;y) là -9.

a) Ta có: 2. (-2) ≤ 3 nên -2 có là nghiệm của bất phương trình

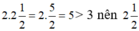+)  không là nghiệm của bất phương trình ,

+) 2π > 3 nên π không là nghiệm của bất phương trình.

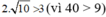+)  nên √10 không là nghiệm của bất phương trình,

Các số là nghiệm của bất phương trình trên là: -2;

Các số không là nghiệm của bất phương trình trên là: 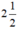; π; √10

b)2x ≤ 3 ⇔ x ≤ 3/2

Biểu diễn tập nghiệm trên trục số là:

a)

f(x) giao trục tại hai Điểm có hoành độ x₁=-4; x₂=-2

g(x) giao trục hoành duy nhất một điểm hoành độ x=m/2

b) f(x) >g(x) => điểm m/2 phải trong khoảng (-4,-2)

\(-4< \dfrac{m}{2}< -2\Leftrightarrow-8< m< -4\)

a) f(x) = 2x.(x+2) - (x+2)(x+1) = 2x2 + 4x - (x2 + 3x + 2) = x2 + x - 2

Tam thức x2 + x – 2 có hai nghiệm x1 = -2 và x2 = 1, hệ số a = 1 > 0.

Vậy:

+ f(x) > 0 nếu x > x2 = 1 hoặc x < x1 = -2, hay x ∈ (-∞; -2) ∪ (1; + ∞)

+ f(x) < 0 nếu x1 < x < x2 hay x ∈ (-2; 1)

+ f(x) = 0 nếu x = -2 hoặc x = 1.

b)

* Hàm số y = 2x(x+2) = 2x2 + 4x có đồ thị (C1) là parabol có:

+ Tập xác định: D = R

+ Đỉnh I1( -1; -2)

+ Trục đối xứng: x = -1

+ Giao điểm với trục tung tại gốc tọa độ.

+ Giao điểm với trục hoành tại O(0; 0) và M(-2; 0).

+ Bảng biến thiên:

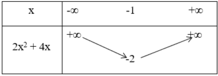
* Hàm số y = (x + 2)(x+1) = x2 + 3x + 2 có đồ thị (C2) là parabol có:

+ Tập xác định D = R.

+ Đỉnh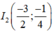 

+ Trục đối xứng: x = -3/2

+ Giao với trục tung tại D(0; 2)

+ Giao với trục hoành tại M(-2; 0) và E(-1; 0)

+ Bảng biến thiên

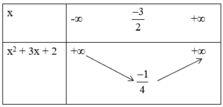
* Đồ thị:

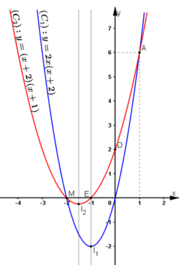
* Tìm tọa độ giao điểm:

Cách 1: Dựa vào đồ thị hàm số:

Nhìn vào đồ thị thấy (C1) cắt (C2) tại A(1; 6) và B ≡ M(-2; 0)

Cách 2: Tính:

Hoành độ giao điểm của (C1) và (C2) là nghiệm của phương trình:

2x(x + 2) = (x + 2)(x + 1)

⇔ (x + 2).2x – (x + 2)(x + 1) = 0

⇔ (x + 2).(2x – x – 1) = 0

⇔ (x + 2).(x – 1) = 0

⇔ x = -2 hoặc x = 1.

+ x = -2 ⇒ y = 0. Ta có giao điểm B(-2; 0)

+ x = 1 ⇒ y = 6. Ta có giao điểm A(1; 6).

c)

+ Đồ thị hàm số y = ax2 + bx + c đi qua điểm A(1; 6) và B(-2; 0)

⇔ tọa độ A và B thỏa mãn phương trình y = ax2 + bx + c

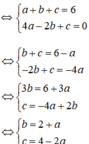
+ Ta có bảng biến thiên của hàm số y = ax2 + bx + c:

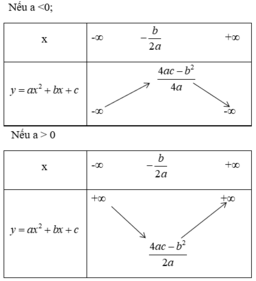
Nhận thấy y đạt giá trị lớn nhất bằng 8

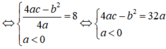
Thay b = 2 + a và c = 4 – 2a vào biểu thức 4ac – b2 = 32a ta được:

4.a.(4 – 2a) – (2 + a)2 = 32a

⇔ 16a – 8a2 – (a2 + 4a + 4) = 32a

⇔ 16a– 8a2 – a2 – 4a - 4 – 32a = 0

⇔ -9a2 - 20a - 4 = 0

⇔ a = -2 hoặc a = -2/9.

Nếu a = -2 ⇒ b = 0, c = 8, hàm số y = -2x2 + 8

Nếu a = -2/9 ⇒ b = 16/9, c = 40/9, hàm số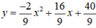 

Vẽ đồ thị:

- Vẽ đồ thị hàm số y = f(x) = x + 1 qua hai điểm (0; 1) và (-1; 0).

- Vẽ đồ thị hàm số y = g(x) = 3 - x qua hai điểm (0; 3) và (3; 0)

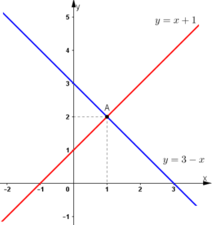
a) Nghiệm của phương trình f(x) = g(x) chính là hoành độ giao điểm của hai đường thẳng y = f(x) và y = g(x).

Giao điểm của hai đường thẳng y = x + 1 và y = 3 – x là điểm A(1; 2).

Do đó phương trình f(x) = g(x) có nghiệm x = 1.

Kiểm tra bằng tính toán:

f(x) = g(x) ⇔ x + 1 = 3 - x ⇔ 2x = 2 ⇔ x = 1.

b) Khi x > 1 thì đồ thị hàm số y = f(x) nằm phía trên đồ thị hàm số y = g(x), hay với x > 1 thì f(x) > g(x).

Kiểm tra bằng tính toán:

f(x) > g(x) ⇔ x + 1 > 3 - x ⇔ 2x > 2 ⇔ x > 1.

c) Khi x < 1 thì đồ thị hàm số y = f(x) nằm phía dưới đồ thị hàm số y = g(x), hay với x < 1 thì f(x) < g(x).

Kiểm tra bằng tính toán:

f(x) < g(x) ⇔ x + 1 < 3 - x ⇔ 2x < 2 ⇔ x < 1.