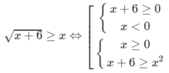
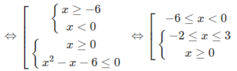
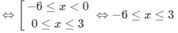
2 2 x - 2 . 2 x + 8 < 2 3 x . 2 1 - x ⇔ 2 2 x + 2 . 2 x - 8 > 0

Đặt t = 4 x (t > 0), ta có hệ bất phương trình:

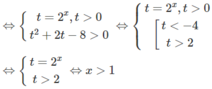
Điều kiện x > 0. Khi đó bất phương trình đã cho tương đương với

log[x(x + 9)] > 1 ⇔ x(x + 9) > 10 ⇔  x 2 + 9 x - 10 > 0

⇔ x < -10 hoặc x > 1 ⇔ x > 1 (do x > 0)

Chọn A

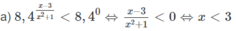
b)  2 x - 2  > 2 2 x + 1

⇔ |x−2| > 2|x+1|

⇔ x 2  − 4x + 4 > 4( x 2  + 2x + 1)

⇔ 3 x 2  + 12x < 0

⇔ −4 < x < 0

c) 2 2 x  − 2. 2 x  + 8 < 2 3 x . 2 1 - x

⇔  2 2 x  + 2. 2 x  − 8 > 0

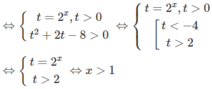
d) Đặt t = 3 x  (t > 0) , ta có bất phương trình

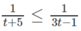
Vì vế trái dương nên vế phải cũng phải dương, tức là 3t - 1 > 0.

Từ đó ta có hệ:

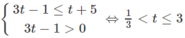
Do đó 1/3 < 3x ≤ 3. Vậy −1 < x ≤ 1.

a) 3 x - 2  < 3 2

⇔ |x − 2| < 2

⇔ −2 < x – 2 < 2

⇔ 0 < x < 4

b) 4 x + 1  > 4 2

⇔ |x + 1| > 2

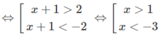
c) 2 - x 2 + 3 x  < 2 2

⇔ − x 2  + 3x < 2

⇔ x 2  − 3x + 2 > 0

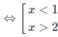
d)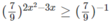 

⇔ 2 x 2  − 3x ≤ −1

⇔ 2 x 2  − 3x + 1 ≤ 0 ⇔ 12 ≤ x ≤ 1

e)

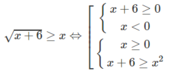
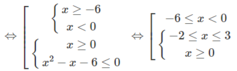
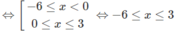
g)

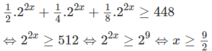
h) Đặt t = 4 x  (t > 0), ta có hệ bất phương trình:

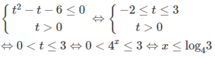
i)

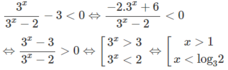
Vẽ đồ thị của hàm số y =  log 2 x  và đường thẳng y = 6 – x trên cùng một hệ trục tọa độ, ta thấy chúng cắt nhau tại điểm có hoành độ x = 4 (H.68).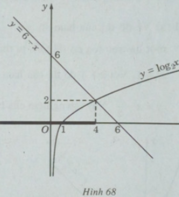Khi x < 4, đồ thị của hàm số y = log 2 x nằm phía dưới y = 6 – x . Vậy tập nghiệm của bất phương trình đã cho là (- ∞ ;4].

3 x - 2 < 3 2

⇔ |x − 2| < 2

⇔ −2 < x – 2 < 2

⇔ 0 < x < 4

4 x + 1 > 4 2

⇔ |x + 1| > 2

⇔ 2 x 2  − 3x ≤ −1

⇔ 2 x 2  − 3x + 1  ≤  0 ⇔ 12  ≤  x  ≤  1