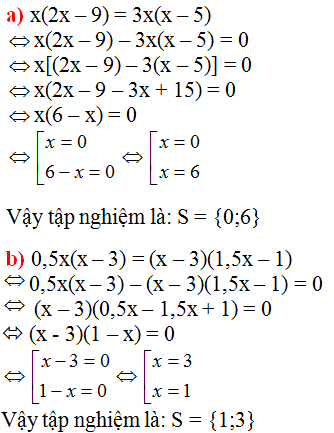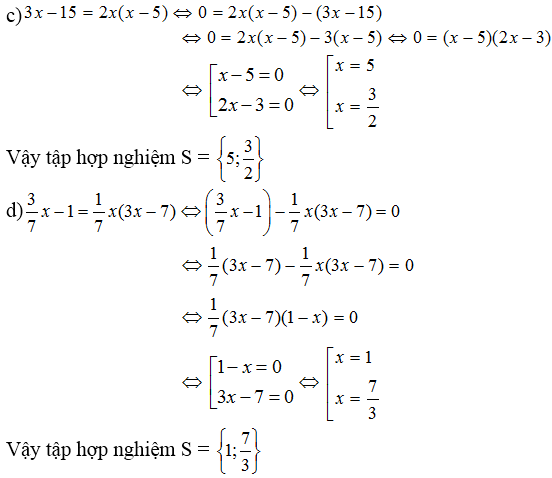a) Ta có: \(\left(2x-3\right)^2=\left(2x-3\right)\left(x+1\right)\)

\(\Leftrightarrow\left(2x-3\right)^2-\left(2x-3\right)\left(x+1\right)=0\)

\(\Leftrightarrow\left(2x-3\right)\left(2x-3-x-1\right)=0\)

\(\Leftrightarrow\left(2x-3\right)\left(x-4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=3\\x=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=4\end{matrix}\right.\)

Vậy: \(S=\left\{\dfrac{3}{2};4\right\}\)

b) Ta có: \(x\left(2x-9\right)=3x\left(x-5\right)\)

\(\Leftrightarrow x\left(2x-9\right)-3x\left(x-5\right)=0\)

\(\Leftrightarrow x\left(2x-9\right)-x\left(3x-15\right)=0\)

\(\Leftrightarrow x\left(2x-9-3x+15\right)=0\)

\(\Leftrightarrow x\left(6-x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\6-x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\)

Vậy: S={0;6}

c) Ta có: \(3x-15=2x\left(x-5\right)\)

\(\Leftrightarrow3\left(x-5\right)-2x\left(x-5\right)=0\)

\(\Leftrightarrow\left(x-5\right)\left(3-2x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-5=0\\3-2x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\2x=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{3}{2}\end{matrix}\right.\)

Vậy: \(S=\left\{5;\dfrac{3}{2}\right\}\)

d) Ta có: \(\dfrac{5-x}{2}=\dfrac{3x-4}{6}\)

\(\Leftrightarrow6\left(5-x\right)=2\left(3x-4\right)\)

\(\Leftrightarrow30-6x=6x-8\)

\(\Leftrightarrow30-6x-6x+8=0\)

\(\Leftrightarrow-12x+38=0\)

\(\Leftrightarrow-12x=-38\)

\(\Leftrightarrow x=\dfrac{19}{6}\)

Vậy: \(S=\left\{\dfrac{19}{6}\right\}\)

e) Ta có: \(\dfrac{3x+2}{2}-\dfrac{3x+1}{6}=2x+\dfrac{5}{3}\)

\(\Leftrightarrow\dfrac{3\left(3x+2\right)}{6}-\dfrac{3x+1}{6}=\dfrac{12x}{6}+\dfrac{10}{6}\)

\(\Leftrightarrow6x+4-3x-1=12x+10\)

\(\Leftrightarrow3x+3-12x-10=0\)

\(\Leftrightarrow-9x-7=0\)

\(\Leftrightarrow-9x=7\)

\(\Leftrightarrow x=-\dfrac{7}{9}\)

Vậy: \(S=\left\{-\dfrac{7}{9}\right\}\)

Với \(x=0\) không phải nghiệm

Với \(x\ne0\) chia 2 vế cho \(x^2\), pt tương đương:

\(2x^2+3x-1+\dfrac{3}{x}+\dfrac{2}{x^2}=0\)

\(\Leftrightarrow2\left(x+\dfrac{1}{x}\right)^2+3\left(x+\dfrac{1}{x}\right)-5=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{x}=1\\x+\dfrac{1}{x}=-\dfrac{5}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2-x+1=0\\2x^2+5x+2=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}=0\left(vô-nghiệm\right)\\\left(x+2\right)\left(2x+1\right)=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-\dfrac{1}{2}\end{matrix}\right.\)

Câu a chắc là đề sai, vì nghiệm vô cùng xấu, tử số của phân thức cuối cùng là \(x+17\) mới hợp lý

b.

Đặt \(x+3=t\) 

\(\Rightarrow\left(t+1\right)^4+\left(t-1\right)^4=14\)

\(\Leftrightarrow t^4+6t^2-6=0\) (đến đây đoán rằng bạn tiếp tục ghi sai đề, nhưng thôi cứ giải tiếp)

\(\Rightarrow\left[{}\begin{matrix}t^2=-3+\sqrt{15}\\t^2=-3-\sqrt{15}\left(loại\right)\end{matrix}\right.\)

\(\Rightarrow t=\pm\sqrt{-3+\sqrt{15}}\Rightarrow x=-3\pm\sqrt{-3+\sqrt{15}}\)

Câu c chắc cũng sai đề, vì lên lớp 8 rồi không ai cho đề kiểu này cả, người ta sẽ rút gọn luôn số 1 bên trái và 60 bên phải.

a: =>|x-7|=3-2x

\(\Leftrightarrow\left\{{}\begin{matrix}x< =\dfrac{3}{2}\\\left(-2x+3\right)^2-\left(x-7\right)^2=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x< =\dfrac{3}{2}\\\left(2x-3-x+7\right)\left(2x-3+x-7\right)=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x< =\dfrac{3}{2}\\\left(x+4\right)\left(3x-10\right)=0\end{matrix}\right.\Leftrightarrow x=-4\)

b: =>|2x-3|=4x+9

\(\Leftrightarrow\left\{{}\begin{matrix}x>=-\dfrac{9}{4}\\\left(4x+9-2x+3\right)\left(4x+9+2x-3\right)=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x>=-\dfrac{9}{4}\\\left(2x+12\right)\left(6x+6\right)=0\end{matrix}\right.\Leftrightarrow x=-1\)

c: =>3x+5=2-5x hoặc 3x+5=5x-2

=>8x=-3 hoặc -2x=-7

=>x=-3/8 hoặc x=7/2

a: =>10x-4=15-9x

=>19x=19

hay x=1

b: \(\Leftrightarrow3\left(10x+3\right)=36+4\left(8x+6\right)\)

=>30x+9=36+32x+24

=>30x-32x=60-9

=>-2x=51

hay x=-51/2

c: \(\Leftrightarrow2x+\dfrac{6}{5}=5-\dfrac{13}{5}-x\)

=>3x=6/5

hay x=2/5

d: \(\Leftrightarrow\dfrac{7x}{8}-\dfrac{5\left(x-9\right)}{1}=\dfrac{20x+1.5}{6}\)

\(\Leftrightarrow21x-120\left(x-9\right)=4\left(20x+1.5\right)\)

=>21x-120x+1080=80x+60

=>-179x=-1020

hay x=1020/179

e: \(\Leftrightarrow5\left(7x-1\right)+60x=6\left(16-x\right)\)

=>35x-5+60x=96-6x

=>95x+6x=96+5

=>x=1

f: \(\Leftrightarrow6\left(x+4\right)+30\left(-x+4\right)=10x-15\left(x-2\right)\)

=>6x+24-30x+120=10x-15x+30

=>-24x+96=-5x+30

=>-19x=-66

hay x=66/19

Bài `1:`

`h)(3/4x-1)(5/3x+2)=0`

`=>[(3/4x-1=0),(5/3x+2=0):}=>[(x=4/3),(x=-6/5):}`

______________

Bài `2:`

`b)3x-15=2x(x-5)`

`<=>3(x-5)-2x(x-5)=0`

`<=>(x-5)(3-2x)=0<=>[(x=5),(x=3/2):}`

`d)x(x+6)-7x-42=0`

`<=>x(x+6)-7(x+6)=0`

`<=>(x+6)(x-7)=0<=>[(x=-6),(x=7):}`

`f)x^3-2x^2-(x-2)=0`

`<=>x^2(x-2)-(x-2)=0`

`<=>(x-2)(x^2-1)=0<=>[(x=2),(x^2=1<=>x=+-2):}`

`h)(3x-1)(6x+1)=(x+7)(3x-1)`

`<=>18x^2+3x-6x-1=3x^2-x+21x-7`

`<=>15x^2-23x+6=0<=>15x^2-5x-18x+6=0`

`<=>(3x-1)(5x-1)=0<=>[(x=1/3),(x=1/5):}`

`j)(2x-5)^2-(x+2)^2=0`

`<=>(2x-5-x-2)(2x-5+x+2)=0`

`<=>(x-7)(3x-3)=0<=>[(x=7),(x=1):}`

`w)x^2-x-12=0`

`<=>x^2-4x+3x-12=0`

`<=>(x-4)(x+3)=0<=>[(x=4),(x=-3):}`

`m)(1-x)(5x+3)=(3x-7)(x-1)`

`<=>(1-x)(5x+3)+(1-x)(3x-7)=0`

`<=>(1-x)(5x+3+3x-7)=0`

`<=>(1-x)(8x-4)=0<=>[(x=1),(x=1/2):}`

`p)(2x-1)^2-4=0`

`<=>(2x-1-2)(2x-1+2)=0`

`<=>(2x-3)(2x+1)=0<=>[(x=3/2),(x=-1/2):}`

`r)(2x-1)^2=49`

`<=>(2x-1-7)(2x-1+7)=0`

`<=>(2x-8)(2x+6)=0<=>[(x=4),(x=-3):}`

`t)(5x-3)^2-(4x-7)^2=0`

`<=>(5x-3-4x+7)(5x-3+4x-7)=0`

`<=>(x+4)(9x-10)=0<=>[(x=-4),(x=10/9):}`

`u)x^2-10x+16=0`

`<=>x^2-8x-2x+16=0`

`<=>(x-2)(x-8)=0<=>[(x=2),(x=8):}`

\(i.\dfrac{\left(2x+1\right)^2}{5}-\dfrac{\left(x-1\right)^2}{3}=\dfrac{7x^2-14x-5}{15}\)

\(\Leftrightarrow\dfrac{4x^2+4x+1}{5}-\dfrac{x^2-2x+1}{3}=\dfrac{7x^2-14x-5}{15}\)

\(\Leftrightarrow\dfrac{12x^2+12x+3}{15}-\dfrac{5x^2-10x+5}{15}=\dfrac{7x^2-14x-5}{15}\)

\(\Leftrightarrow12x^2+12x+3-5x^2+10x-5=7x^2-14x-5\)

\(\Leftrightarrow36x=-3\)

\(\Leftrightarrow x=-\dfrac{1}{12}\)

\(k.x+\dfrac{2x+\dfrac{x-1}{5}}{3}=1-\dfrac{3x-\dfrac{1-2x}{3}}{5}\)

\(\Leftrightarrow\dfrac{15x}{15}+\dfrac{10x+x-1}{15}=\dfrac{15}{15}-\dfrac{9x-1+2x}{15}\)

\(\Leftrightarrow15x+9x-1=14-7x\)

\(\Leftrightarrow31x=15\)

\(\Leftrightarrow x=\dfrac{15}{31}\)

a) $\frac{1}{x-1}-\frac{3x^2}{x^3-1}=\frac{2x}{x^2+x+1}$

Ta có: $x^3-1=\left(x-1\right)\left(x^2+x+1\right)$

$=\left(x-1\right)\left[{\left(x+\frac{1}{2}\right)}^2+\frac{3}{4}\right]$ cho nên x³ – 1 ≠ 0 khi x – 1 ≠ 0⇔ x ≠ 1

Vậy ĐKXĐ: x ≠ 1

Khử mẫu ta được:

$x^2+x+1-3x^2=2x\left(x-1\right)\iff -2x^2+x+1=2x^2-2x$

$\iff 4x^2-3x-1=0$

$\iff 4x(x-1$