Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

BÀI 1. Giải các phương trình sau bằng công thức nghiệm hoặc (công thức nghiện thu gọn).
1) x2 - 11x + 38 = 0 ;
2) 6x2 + 71x + 175 = 0 ;
3) 5x2 - 6x + 27 =0 ;
4) - 30x2 + 30x - 7,5 = 0 ;
5) 4x2 - 16x + 17 = 0 ;
6) x2 + 4x - 12 = 0 ;

A=(x1-x2)^2-x1^2+x1(x1+x2)
=(x1-x2)^2+x1x2
=(x1+x2)^2-x1x2
=(1/2)^2-(-1/4)=1/4+1/4=1/2

a ) x 2 – 5 = 0 ⇔ x 2 = 5 ⇔ x 1 = √ 5 ; x 2 = - √ 5
Vậy phương trình có hai nghiệm x 1 = √ 5 ; x 2 = - √ 5
Cách khác:
x 2 – 5 = 0 ⇔ x 2 – ( √ 5 ) 2 = 0
⇔ (x - √5)(x + √5) = 0
hoặc x - √5 = 0 ⇔ x = √5
hoặc x + √5 = 0 ⇔ x = -√5
b)
x 2 – 2 √ 11 x + 11 = 0 ⇔ x 2 – 2 √ 11 x + ( √ 11 ) 2 = 0 ⇔ ( x - √ 11 ) 2 = 0
⇔ x - √11 = 0 ⇔ x = √11
Vậy phương trình có một nghiệm là x = √11

\(\hept{\begin{cases}x_1+x_2=2\\x_1.x_2=-5\end{cases}}\)
\(B=x_1^2+x_2^2=\left(x_2+x_2\right)^2-2x_1.x_2=2^2+2.5=14\)
Câu C phân tích tương tự
Cho phương trình: 5 x^2-2\sqrt{5}x+1 = 05x2−25x+1=0.
Điền số thích hợp vào ô trống:
Biệt thức \Delta=Δ=
×
.
Nghiệm x=x=

a, \(x^4-4x^3-6x^2-4x+1=0\)(*)
<=> \(x^4+4x^2+1-4x^3-4x+2x^2-12x^2=0\)
<=> \(\left(x^2-2x+1\right)^2=12x^2\)
<=>\(\left(x-1\right)^4=12x^2\) <=> \(\left[{}\begin{matrix}\left(x-1\right)^2=\sqrt{12}x\\\left(x-1\right)^2=-\sqrt{12}x\end{matrix}\right.\)<=> \(\left[{}\begin{matrix}x^2-2x+1-\sqrt{12}x=0\left(1\right)\\x^2-2x+1+\sqrt{12}x=0\left(2\right)\end{matrix}\right.\)
Giải (1) có: \(x^2-2x+1-\sqrt{12}x=0\)
<=> \(x^2-2x\left(1+\sqrt{3}\right)+\left(1+\sqrt{3}\right)^2-\left(1+\sqrt{3}\right)^2+1=0\)
<=> \(\left(x-1-\sqrt{3}\right)^2-3-2\sqrt{3}=0\)
<=> \(\left(x-1-\sqrt{3}\right)^2=3+2\sqrt{3}\) <=> \(\left[{}\begin{matrix}x-1-\sqrt{3}=\sqrt{3+2\sqrt{3}}\\x-1-\sqrt{3}=-\sqrt{3+2\sqrt{3}}\end{matrix}\right.\) <=> \(\left[{}\begin{matrix}x=\sqrt{3+2\sqrt{3}}+\sqrt{3}+1\left(ktm\right)\\x=-\sqrt{3+2\sqrt{3}}+\sqrt{3}+1\left(tm\right)\end{matrix}\right.\)
=> \(x=-\sqrt{3+2\sqrt{3}}+\sqrt{3}+1\)
Giải (2) có: \(x^2-2x+1+\sqrt{12}x=0\)
<=> \(x^2-2x\left(1-\sqrt{3}\right)+\left(1-\sqrt{3}\right)^2-\left(1-\sqrt{3}\right)^2+1=0\)
<=> \(\left(x+\sqrt{3}-1\right)^2=3-2\sqrt{3}\) .Có VP<0 => PT (2) vô nghiệm
Vậy pt (*) có nghiệm x=\(-\sqrt{3+2\sqrt{3}}+\sqrt{3}+1\)
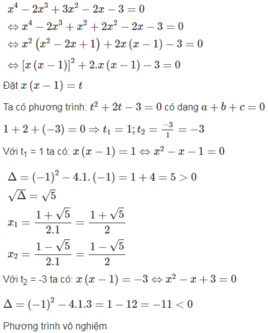

câu d, xem lại đề bài nha!