Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\sqrt{x^{ }2-6x+9}=4-x\)
\(\sqrt{\left(x-3\right)^{ }2}=4-x\)
x-3=4-x
x+x=4+3
2x=7
x=\(\dfrac{7}{2}\)
Lời giải:
a.
PT \(\Leftrightarrow \left\{\begin{matrix} 4-x\geq 0\\ x^2-6x+9=(4-x)^2=x^2-8x+16\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\leq 4\\ 2x=7\end{matrix}\right.\Leftrightarrow x=\frac{7}{2}\)
b.
ĐKXĐ: $x\geq \frac{3}{2}$
PT \(\Leftrightarrow \sqrt{(2x-3)+2\sqrt{2x-3}+1}+\sqrt{(2x-3)+8\sqrt{2x-3}+16}=5\)
\(\Leftrightarrow \sqrt{(\sqrt{2x-3}+1)^2}+\sqrt{(\sqrt{2x-3}+4)^2}=5\)
\(\Leftrightarrow |\sqrt{2x-3}+1|+|\sqrt{2x-3}+4|=5\)
\(\Leftrightarrow \sqrt{2x-3}+1+\sqrt{2x-3}+4=2\sqrt{2x-3}+5=5\)
\(\Leftrightarrow \sqrt{2x-3}=0\Leftrightarrow x=\frac{3}{2}\)

\(2x^2-6x-3=0\)
\(\Delta'=\left(-3\right)^2+3.2=15>0\)
⇒ Phương trình có hai nghiệm phân biệt với mọi m.
Theo hệ thức viét ta có : \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1.x_2=-\dfrac{3}{2}\end{matrix}\right.\)
Ta có : \(B=3x_1x_2-x_1^2-x_2^2=-\left(x_1+x_2\right)^2+5x_1x_2=-9+5.\left(-\dfrac{3}{2}\right)=\dfrac{135}{2}\)
Vậy \(B=-\dfrac{135}{2}\) với hai nghiệm phân biệt thỏa mãn.

\(2x^2-6x-3=0\)
\(\Delta'=3^2+3.2=15>0\)
⇒ Phương trình có hai nghiệm phân biệt.
Theo hệ thức viét có : \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=-\dfrac{3}{2}\end{matrix}\right.\)
Ta có : \(A=x_1^2x_2^2-2x_1-2x_2=\left(x_1x_2\right)^2-2\left(x_1+x_2\right)=\left(-\dfrac{3}{2}\right)^2-2.3=-\dfrac{15}{4}\)
Vậy \(A=-\dfrac{15}{4}\) thì thỏa mãn điều kiện bài ra.

Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{6}{2}=-3\\x_1x_2=\dfrac{-3}{2}\end{matrix}\right.\)
Ta có: \(\dfrac{2}{x_1^2}+\dfrac{2}{x_2^2}\)
\(=\dfrac{2x^2_2+2x_1^2}{\left(x_1\cdot x_2\right)^2}\)
\(=\dfrac{2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]}{\left(-\dfrac{3}{2}\right)^2}=\dfrac{2\cdot\left[\left(-3\right)^2-2\cdot\dfrac{-3}{2}\right]}{\dfrac{9}{4}}\)
\(=\dfrac{2\cdot12}{\dfrac{9}{4}}=24\cdot\dfrac{4}{9}=\dfrac{96}{9}=\dfrac{32}{3}\)

\(\left\{{}\begin{matrix}x^2+2xy-3y^2=-4\left(1\right)\\2x^2+xy+4y^2=5\left(2\right)\end{matrix}\right.\)\(với\)\(y=0\Rightarrow hpt\Leftrightarrow\left\{{}\begin{matrix}x^2=-4\\2x^2=5\end{matrix}\right.\)\(\left(loại\right)\)
\(y\ne0\) \(đặt:x=t.y\Rightarrow hpt\Leftrightarrow\left\{{}\begin{matrix}t^2y^2+2ty^2-3y^2=-4\left(3\right)\\2t^2y^2+ty^2+4y^2=5\left(4\right)\end{matrix}\right.\)
\(\Leftrightarrow5t^2y^2+10ty^2-15y^2=-8t^2y^2-4ty^2-16y^2\)
\(\Leftrightarrow13t^2y^2+14ty^2+y^2=0\)
\(\Leftrightarrow13t^2+14t+1=0\Leftrightarrow\left[{}\begin{matrix}t=-\dfrac{1}{13}\\t=-1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{13}y\left(5\right)\\x=-y\left(6\right)\end{matrix}\right.\)
\(thay\left(5\right)và\left(6\right)\) \(lên\left(1\right)hoặc\left(2\right)\Rightarrow\left(x;y\right)=\left\{\left(1;-1\right);\left(-1;1\right);\left(-\dfrac{1}{\sqrt{133}};\dfrac{13}{\sqrt{133}}\right)\right\}\)
\(pt:x^4-4x^3+x^2+6x+m+2=0\)
\(\Leftrightarrow x^4-4x^3+4x^2-3x^2+6x+m+2=0\)
\(\Leftrightarrow\left(x^2-2x\right)^2-3\left(x^2-2x\right)+m+2=0\left(1\right)\)
\(đặt:x^2-2x=t\ge-1\)
\(\Rightarrow\left(1\right)\Leftrightarrow t^2-3t=-m-2\)
\(xét:f\left(t\right)=t^2-3t\) \(trên[-1;+\text{∞})\) \(và:y=-m-2\)
\(\Rightarrow f\left(-1\right)=4\)
\(f\left(-\dfrac{b}{2a}\right)=-\dfrac{9}{4}\)
\(\left(1\right)\) \(có\) \(3\) \(ngo\) \(pb\Leftrightarrow-m-2=4\Leftrightarrow m=-6\)
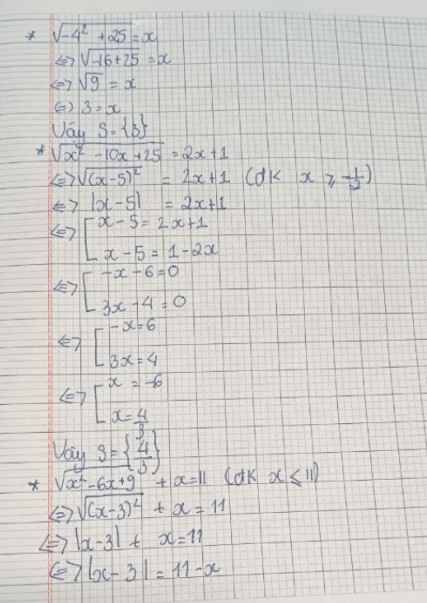
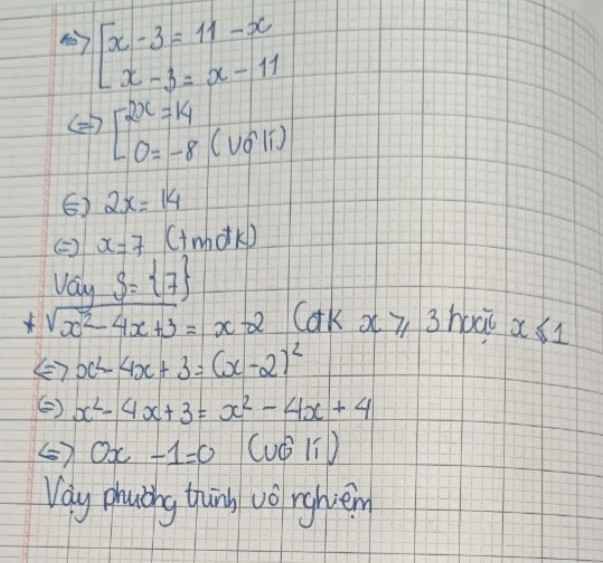
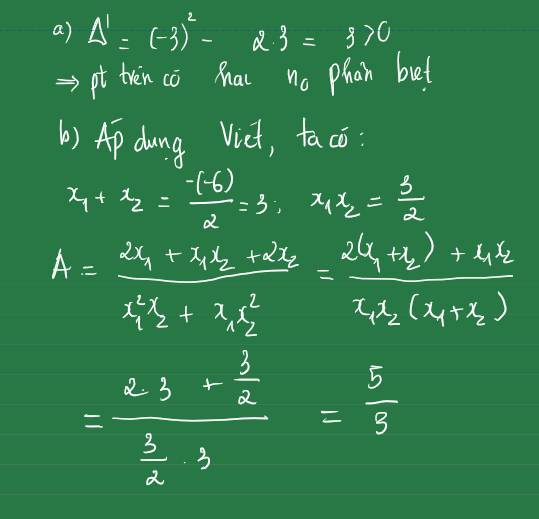
a: =>|x-3|=4-x
\(\Leftrightarrow\left\{{}\begin{matrix}x< =4\\\left(4-x-x+3\right)\left(4-x+x-3\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x< =4\\\left(7-2x\right)=0\end{matrix}\right.\Leftrightarrow x=\dfrac{7}{2}\)
b: =>|x-5|=3-19x
\(\Leftrightarrow\left\{{}\begin{matrix}x< =\dfrac{3}{19}\\\left(x-5-3+19x\right)\left(x-5+3-19x\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x< =\dfrac{3}{19}\\\left(20x-8\right)\left(-18x-2\right)=0\end{matrix}\right.\Leftrightarrow x\in\left\{-\dfrac{1}{9}\right\}\)
c: =>\(\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}+\sqrt{x-3}\right)=0\)
=>căn x-3=0
=>x=3