
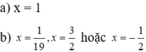
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

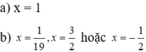

a) \(\dfrac{3}{x-7}+\dfrac{2}{x+7}=\dfrac{5}{x^2-49}\)
(ĐKXĐ: x khác 7; x khác -7)
<=>\(\dfrac{3.\left(x+7\right)}{\left(x-7\right).\left(x+7\right)}+\dfrac{2.\left(x-7\right)}{\left(x+7\right).\left(x-7\right)}=\dfrac{5}{\left(x+7\right).\left(x-7\right)}\)
=> 3x + 21 + 2x - 14 = 5
<=> 3x + 2x = 5 + 14 - 21
<=> 5x = -2
<=> x = \(\dfrac{-2}{5}\)
Vậy S = { \(\dfrac{-2}{5}\) }
b) \(\dfrac{2x-1}{3}-\dfrac{x+3}{2}>1+\dfrac{5x}{6}\)
<=> \(\dfrac{2.\left(2x-1\right)}{3.2}-\dfrac{3.\left(x+3\right)}{3.2}>\dfrac{1.6}{6}+\dfrac{5x}{6}\)
=> 4x - 2 - 3x - 9 > 6 + 5x
<=> 4x - 3x - 5x > 6 + 9 + 2
<=> -4x > 17
<=> \(\dfrac{-17}{4}\)
Vậy S = { \(\dfrac{-17}{4}\) }

b) Đặt \(x^2+2x+3=a\)(a>0)
Ta có: \(\dfrac{x^2+2x+7}{\left(x+1\right)^2+2}=x^2+2x+4\)
\(\Leftrightarrow\dfrac{x^2+2x+7}{x^2+2x+1+2}=x^2+2x+4\)
\(\Leftrightarrow\dfrac{x^2+2x+7}{x^2+2x+3}=x^2+2x+4\)
\(\Leftrightarrow\dfrac{a+4}{a}=a+1\)
\(\Leftrightarrow a^2+a=a+4\)
\(\Leftrightarrow a^2=4\)
\(\Leftrightarrow\left[{}\begin{matrix}a=2\left(nhận\right)\\a=-2\left(loại\right)\end{matrix}\right.\)
\(\Leftrightarrow x^2+2x+3=2\)
\(\Leftrightarrow x^2+2x+1=0\)
\(\Leftrightarrow\left(x+1\right)^2=0\)
\(\Leftrightarrow x+1=0\)
hay x=-1
Vậy: S={-1}
ĐKXĐ của cả 2 pt trên đều là `x in RR`
`a,1/(x^2-2x+2)+2/(x^2-2x+3)=6/(x^2-2x+4)`
Đặt `a=x^+2x+3(a>=2)` ta có:
`1/(a-1)+2/a=6/(a+1)`
`<=>a(a+1)+2(a-1)(a+1)=6a(a-1)`
`<=>a^2+a+2(a^2-1)=6a^2-6a`
`<=>a^2+a+2a^2-2=6a^2-6a`
`<=>3a^2-5a+2=0`
`<=>3a^2-3a-2a+2=0`
`<=>3a(a-1)-2(a-1)=0`
`<=>(a-1)(3a-2)=0`
`a>=2=>a-1>=1>0`
`a>=2=>3a-2>=4>0`
Vậy pt vô nghiệm
`(x^2+2x+7)/((x+1)^2+2)=x^2+2x+4`
`<=>(x^2+2x+7)=(x^2+2x+4)(x^2+2x+3)`
Đặt `a=x^2+2x+3(a>=2)`
`pt<=>a+4=a(a+1)`
`<=>a^2+a=a+4`
`<=>a^2=4`
`<=>a=2` do `a>=2`
`<=>(x+1)^2+2=2`
`<=>(x+1)^2=0`
`<=>x=-1`
Vậy `S={-1}`

a) Ta có: \(\left|x^2-x+2\right|-3x-7=0\)
\(\Leftrightarrow\left|x^2-x+2\right|=3x+7\)
\(\Leftrightarrow x^2-x+2=3x+7\)(Vì \(x^2-x+2>0\forall x\))
\(\Leftrightarrow x^2-x+2-3x-7=0\)
\(\Leftrightarrow x^2-4x-5=0\)
\(\Leftrightarrow x^2-5x+x-5=0\)
\(\Leftrightarrow x\left(x-5\right)+\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
Vậy: S={5;-1}
bạn giải giúp mình câu b nữa với
mai mình phải nộp bài rồi!!!![]()

a,\(\left(x-4-5\right)\left(x-4+5\right)=0\Leftrightarrow\left(x-9\right)\left(x+1\right)=0\Leftrightarrow x=9;x=-1\)
b, \(\left(x-3-x-1\right)\left(x-3+x+1\right)=0\Leftrightarrow2x-2=0\Leftrightarrow x=1\)
c, \(\left(x^2-4\right)\left(2x-3\right)-\left(x^2-4\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left(x^2-4\right)\left(2x-3-x+1\right)=0\Leftrightarrow\left(x-2\right)\left(x+2\right)\left(x-2\right)=0\Leftrightarrow x=-2;x=2\)
d, \(\left(3x-7\right)^2-\left(2x+2\right)^2=0\Leftrightarrow\left(3x-7-2x-2\right)\left(3x-7+2x+2\right)=0\)
\(\Leftrightarrow\left(x-9\right)\left(5x-5\right)=0\Leftrightarrow x=1;x=9\)

Mình khuyên bạn thế này :
Bạn nên tách những câu hỏi ra
Như vậy các bạn sẽ dễ giúp
Và cũng có nhiều bạn giúp hơn !
Bài 1.
a) ( x - 3 )( x + 7 ) = 0
<=> x - 3 = 0 hoặc x + 7 = 0
<=> x = 3 hoặc x = -7
Vậy S = { 3 ; -7 }
b) ( x - 2 )2 + ( x - 2 )( x - 3 ) = 0
<=> ( x - 2 )( x - 2 + x - 3 ) = 0
<=> ( x - 2 )( 2x - 5 ) = 0
<=> x - 2 = 0 hoặc 2x - 5 = 0
<=> x = 2 hoặc x = 5/2
Vậy S = { 2 ; 5/2 }
c) x2 - 5x + 6 = 0
<=> x2 - 2x - 3x + 6 = 0
<=> x( x - 2 ) - 3( x - 2 ) = 0
<=> ( x - 2 )( x - 3 ) = 0
<=> x - 2 = 0 hoặc x - 3 = 0
<=> x = 2 hoặc x = 3

Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) đẻ được hỗ trợ tốt hơn. Viết như thế kia rất khó đọc => khả năng bị bỏ qua bài cao.
a: =>3x=3
=>x=1
b: =>12x-2(5x-1)=3(8-3x)
=>12x-10x+2=24-9x
=>2x+2=24-9x
=>11x=22
=>x=2
c: =>2x-3(2x+1)=x-6x
=>-5x=2x-6x-3=-4x-3
=>-x=-3
=>x=3
d: =>2x-5=0 hoặc x+3=0
=>x=5/2 hoặc x=-3
e: =>x+2=0
=>x=-2

x2-4x+7 = 0 ⇔ x2 -4x + 4 + 3 = 0
⇔ (x-2)2+3=0 ⇔ (x-2)2=-3 (vô lí)
Vậy pt vô nghiệm
*Chứng minh phương trình \(x^2-4x+7=0\) vô nghiệm
Ta có: \(x^2-4x+7=0\)
\(\Leftrightarrow x^2-4x+4+3=0\)
\(\Leftrightarrow\left(x-2\right)^2+3=0\)
mà \(\left(x-2\right)^2+3\ge3>0\forall x\)
nên \(x\in\varnothing\)(đpcm)

a) ĐKXĐ: \(x\ne1\)
Ta có: \(\dfrac{7x-3}{x-1}=\dfrac{2}{3}\)
\(\Leftrightarrow3\left(7x-3\right)=2\left(x-1\right)\)
\(\Leftrightarrow21x-9=2x-2\)
\(\Leftrightarrow21x-2x=-2+9\)
\(\Leftrightarrow19x=7\)
\(\Leftrightarrow x=\dfrac{7}{19}\)
Vậy: \(S=\left\{\dfrac{7}{19}\right\}\)