
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
\(P.\frac{1}{\sqrt{2}}=\frac{\sqrt{(x-1)+2\sqrt{x-1}+1}+\sqrt{(x-1)-2\sqrt{x-1}+1}}{\sqrt{(2x-1)+2\sqrt{2x-1}+1}-\sqrt{(2x-1)-2\sqrt{2x-1}+1}}\)
\(=\frac{\sqrt{(\sqrt{x-1}+1)^2}+\sqrt{(\sqrt{x-1}-1)^2}}{\sqrt{(\sqrt{2x-1}+1)^2}-\sqrt{(\sqrt{2x-1}-1)^2}}\)
\(=\frac{\sqrt{x-1}+1+\sqrt{x-1}-1}{\sqrt{2x-1}+1-(\sqrt{2x-1}-1)}=\frac{2\sqrt{x-1}}{2}=\sqrt{x-1}\)

Gọi thời gian làm riêng 1 mình xong con mương của đội (I) và (II) lần lượt là x và y (ngày) với x;y>0
Trong 1 ngày hai đội lần lượt đào được \(\dfrac{1}{x}\) và \(\dfrac{1}{y}\) phần con mương
Do hai đội dự định cùng đào xong trong 10 ngày nên:
\(10\left(\dfrac{1}{x}+\dfrac{1}{y}\right)=1\Rightarrow\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{10}\) (1)
Trong 6 ngày hai đội làm chung được: \(\dfrac{6}{10}=\dfrac{3}{5}\) phần con mương
Do đó trong 4 ngày còn lại đội 2 cần đào \(1-\dfrac{3}{5}=\dfrac{2}{5}\) phần con mương
Năng suất đội 2 gấp đôi đội (I) nên trong 4 ngày đó, mỗi ngày đội 2 đào được \(\dfrac{2}{x}\) phần con mương.
Ta có phương trình: \(4.\dfrac{2}{x}=\dfrac{2}{5}\Rightarrow x=20\)
Thế vào (1) \(\Rightarrow\dfrac{1}{20}+\dfrac{1}{y}=\dfrac{1}{10}\Rightarrow y=20\)
Vậy nếu làm riêng thì mỗi đội phải mất 20 ngày

2:
1+cot^2a=1/sin^2a
=>1/sin^2a=1681/81
=>sin^2a=81/1681
=>sin a=9/41
=>cosa=40/41
tan a=1:40/9=9/40

\(\Delta=\left(-1\right)^2-4.1.\left(-2\right)=9>0\Rightarrow\sqrt{\Delta}=3\)
Vậy PT có 2 nghiệm phân biệt: \(x_1=\frac{-\left(-1\right)+3}{2}=2;x_2=\frac{-\left(-1\right)-3}{2}=-1\)

2.2 Đề lỗi không dịch được
2.3
\(\Delta'=4m^2-2\left(2m^2-1\right)=2>0\Rightarrow\) pt luôn có 2 nghiệm pb
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=\dfrac{2m^2-1}{2}\end{matrix}\right.\)
\(\Rightarrow\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2=2\Rightarrow\left[{}\begin{matrix}x_1-x_2=\sqrt{2}\\x_1-x_2=-\sqrt{2}\end{matrix}\right.\)
Do \(x_1\) là nghiệm của pt nên ta có:
\(2x_1^2-4mx_1+2m^2-1=0\Rightarrow2x_1^2=4mx_1-2m^2+1\)
Thế vào bài toán:
\(4mx_1-2m^2+1-4mx_2+2m^2-9< 0\)
\(\Leftrightarrow m\left(x_1-x_2\right)< 2\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{2}m< 2\\-\sqrt{2}m< 2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m< \sqrt{2}\\m>-\sqrt{2}\end{matrix}\right.\)
(Bản thân câu này đề bài cũng rất dở)

Áp dụng BĐT Cô-si:
\(\dfrac{x^2}{x+1}+\dfrac{x+1}{9}\ge2\sqrt{\dfrac{x^2\left(x+1\right)}{9\left(x+1\right)}}=\dfrac{2}{3}x\)
\(\dfrac{y^2}{y+1}+\dfrac{y+1}{9}\ge2\sqrt{\dfrac{y^2\left(y+1\right)}{9\left(y+1\right)}}=\dfrac{2}{3}y\)
Cộng vế:
\(\dfrac{x^2}{x+1}+\dfrac{y^2}{y+1}+\dfrac{x+y+2}{9}\ge\dfrac{2}{3}\left(x+y\right)\)
\(\Leftrightarrow P+\dfrac{1+2}{9}\ge\dfrac{2}{3}.1\)
\(\Rightarrow P\ge\dfrac{1}{3}\)
\(P_{min}=\dfrac{1}{3}\) khi \(x=y=\dfrac{1}{2}\)

Áp dụng BĐT Cô-si:
\(3\left(a^2+4\right)\ge3.4a=12a\)
\(b^4+b^4+b^4+81\ge4\sqrt[4]{81b^{12}}=12b^3\)
Cộng vế:
\(3\left(a^2+b^4\right)+93\ge12\left(a+b^3\right)=384\)
\(\Rightarrow a^2+b^4\ge85\)
\(\Rightarrow P\ge85-19=66\)
\(P_{min}=66\) khi \(\left(a;b\right)=\left(2;3\right)\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2x-3=2\cdot1-3=-1\end{matrix}\right.\)
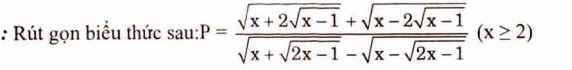







ĐKXĐ: \(\left\{{}\begin{matrix}5x^2+14x+9>=0\\x+1>=0\\x^2-x-20>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(x+1\right)\left(5x+9\right)>=0\\x+1>=0\\\left(x-5\right)\left(x+4\right)>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}x< =-\dfrac{9}{5}\\x>=-1\end{matrix}\right.\\x>=-1\\\left[{}\begin{matrix}x>=5\\x< =-4\end{matrix}\right.\end{matrix}\right.\)
=>x>=5
\(\sqrt{5x^2+14x+9}-\sqrt{x^2-x-20}=5\sqrt{x+1}\)
=>\(\sqrt{5x^2+14x+9}-21+6-\sqrt{x^2-x-20}=5\sqrt{x+1}-15\)
=>\(\dfrac{5x^2+14x+9-441}{\sqrt{5x^2+14x+9}+21}+\dfrac{36-x^2+x+20}{6+\sqrt{x^2-x-20}}=5\left(\sqrt{x+1}-3\right)\)
=>\(\dfrac{5x^2+14x-432}{\sqrt{5x^2+14x+9}+21}+\dfrac{-x^2+x+56}{6+\sqrt{x^2-x-20}}=5\cdot\dfrac{x+1-9}{\sqrt{x+1}+3}\)
=>\(\dfrac{\left(x-8\right)\left(5x+54\right)}{\sqrt{5x^2+14x+9}+21}-\dfrac{x^2-x-56}{\sqrt{x^2-x-20}+6}=\dfrac{5\left(x-8\right)}{\sqrt{x+1}+3}\)
=>\(\dfrac{\left(x-8\right)\left(5x+4\right)}{\sqrt{5x^2+14x+9}+21}-\dfrac{\left(x-8\right)\left(x+7\right)}{\sqrt{x^2-x-20}+6}-\dfrac{5\left(x-8\right)}{\sqrt{x+1}+3}=0\)
=>\(\left(x-8\right)\left(\dfrac{5x+4}{\sqrt{5x^2+14x+9}+21}-\dfrac{x+7}{\sqrt{x^2-x-20}+6}-\dfrac{5}{\sqrt{x+1}+3}\right)=0\)
=>x-8=0
=>x=8(nhận)