
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác AMIN có
\(\widehat{AMI}=\widehat{ANI}=\widehat{MAN}=90^0\)
Do đó: AMIN là hình chữ nhật

Gọi độ dài quãng đường AB là x
Theo đề, ta có phương trình:
\(\dfrac{x}{40}-\dfrac{x}{50}=\dfrac{7}{20}\)
\(\Leftrightarrow x\cdot\dfrac{1}{200}=\dfrac{7}{20}\)
hay x=70

Phương trình bậc 3 thì chịu.
Mình bấm máy tính nó ra x=-3,256674079...
Sau khi giải thì nó ra x3-6x+15=0
Mình dùng phương pháp hệ số bất định để phân tích đa thức thành nhân tử nhưng số xấu lắm, mình cũng không biết có đúng không.


1) \(A=25x^2+10x+1\)
\(A=5x^2+2.5.10x+1\)
\(A=5x^2+100x+1\)
\(A=\left(5x+1\right)^2\)
Thay \(x=\dfrac{1}{5}\) vào biểu thức \(\left(5x+1\right)^2\)
\(\left(5x+1\right)^2\)
= \(\left(5.\dfrac{1}{5}+1\right)^2\)
= \(2^2=4\)
Nếu sai thì cho mình xin lỗi nhé
2) Bài này mình không biết làm

c,\(\dfrac{5-x}{2}-\dfrac{3x+4}{3}=\dfrac{1}{4}\)
⇔\(\dfrac{5-x}{2}+\dfrac{-3x-4}{3}=\dfrac{1}{4}\)
⇔\(\dfrac{6\left(5-x\right)}{12}+\dfrac{4\left(-3x-4\right)}{12}=\dfrac{3}{12}\)
⇔6(5-x)+4(-3x-4)=3
⇔ 30-6x-12x-16=3
⇔ 30-16-3=12x+6x
⇔ 11=18x
⇔ x=\(\dfrac{11}{18}\)
Vậy S=\(\left\{\dfrac{11}{18}\right\}\)
d)x2-5x=9(x-5)
⇔x(x-5)=9(x-5)
⇔x(x-5)-9(x-5)=0
⇔(x-9)(x-5)=0
⇔\(\left\{{}\begin{matrix}x-9=0\Leftrightarrow x=9\\x-5=0\Leftrightarrow x=5\end{matrix}\right.\)
Vậy S=\(\left\{5;9\right\}\)

2)
Đổi 1h15 phút thành 1,25 h
Thời gian dự định là: $\frac{AB}{40}$ (h)
Thời gian thực tế: $\frac{AB}{40-15}=\frac{AB}{25}$ (h)
Chênh lệch thời gian dự định và thời gian thực tế là:
$\frac{AB}{25}-\frac{AB}{40}=1,25$
$\frac{3AB}{200}=1,25\Rightarrow AB=83,33$ (km)
Câu 3:
Đổi 20 phút thành $\frac{1}{3}$ giờ
Giả sử sau khi ô tô đi được $a$ giờ thì hai xe gặp nhau tại $C$. Lúc này, xe máy đã đi được $a+\frac{1}{3}$ giờ
Ta có:
$AC=35(a+\frac{1}{3})=(35+20).a$
$\Leftrightarrow 35(a+\frac{1}{3})=55a$
$\Rightarrow a=\frac{7}{12}$ (h)
Đổi $\frac{7}{12}$ h = 35 phút. Vậy sau khi đi được 35 phút thì ô tô gặp xe máy.








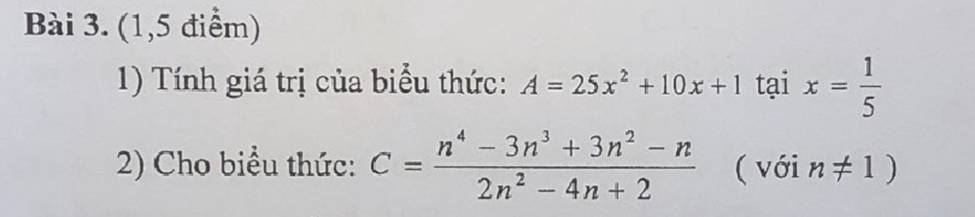 Giải dùm mình với ạ! Mình cần gấp
Giải dùm mình với ạ! Mình cần gấp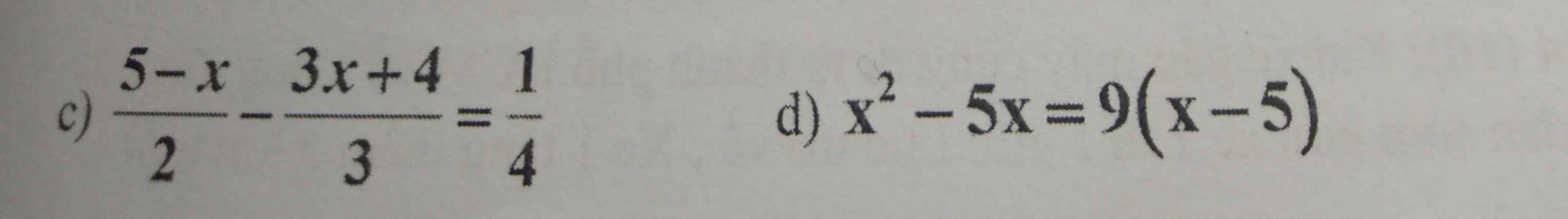

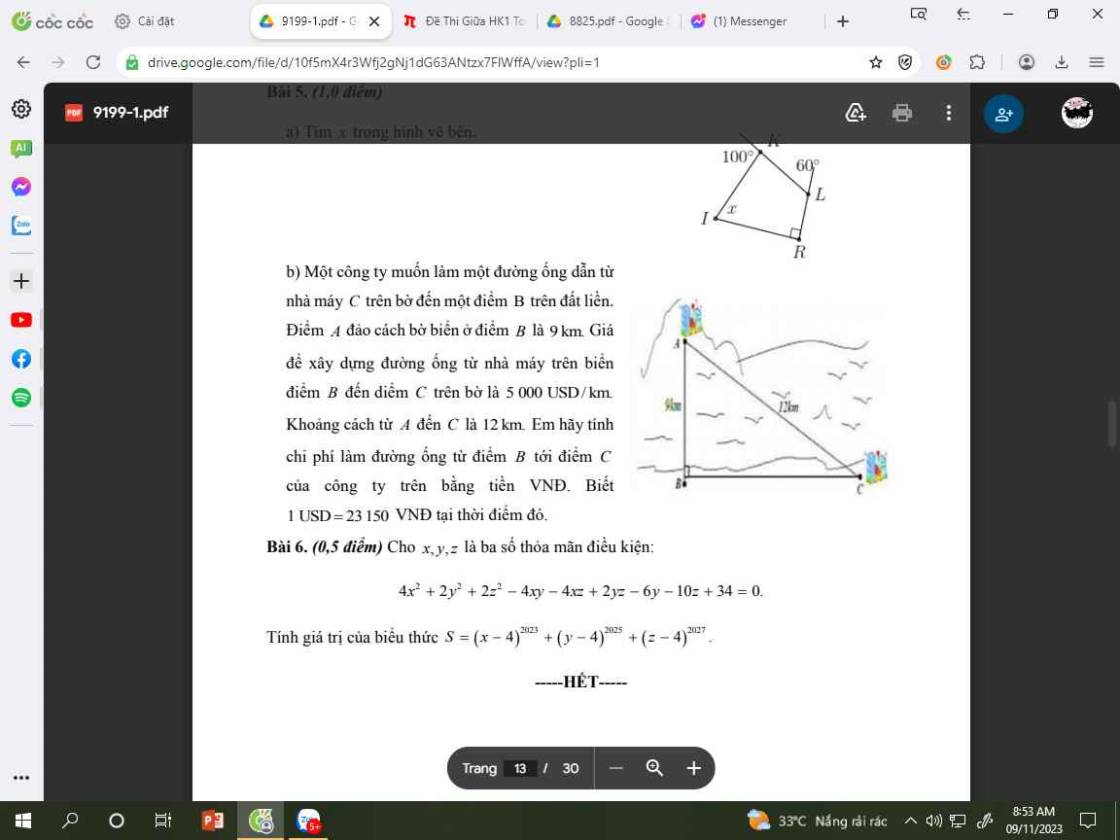
Bài 6: Ta có:
\(4x^2+2y^2+2z^2-4xy-4xz+2yz-6y-10z+34=0\)
\(\Leftrightarrow4x^2+y^2+z^2-4xy-4xz+2yz+y^2-6y+9+z^2-10z+25=0\)
\(\Leftrightarrow\left[\left(2x\right)^2+y^2+z^2-2\cdot2x\cdot y-2\cdot2x\cdot z+2\cdot y\cdot z\right]+\left(y^2-6y+9\right)+\left(z^2-10z+25\right)=0\)
\(\Leftrightarrow\left(2x-y-z\right)^2+\left(y-3\right)^2+\left(z-5\right)^2=0\)
Mà: \(\left(2x-y-z\right)^2+\left(y-3\right)^2+\left(z-5\right)^2\ge0\forall x,y,z\)
Mặt khác: \(\left(2x-y-z\right)^2+\left(y-3\right)^2+\left(z-5\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-y-z=0\\y-3=0\\z-5=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-3-5=0\\y=3\\z=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x=8\\y=3\\z=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=3\\z=5\end{matrix}\right.\)
Thay vào S ta có:
\(S=\left(4-4\right)^{2023}+\left(3-4\right)^{2025}+\left(5-4\right)^{2027}=0-1+1=0\)