
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)

Bạn không chụp hết đề nhưng mình đoán là tìm $m$ để hàm số đồng biến trên $\mathbb{R}$
Lời giải:
Để hàm số đồng biến trên $\mathbb{R}$ thì:
$y'=3mx^2-2(2m-1)x+(m-2)\geq 0, \forall x\in\mathbb{R}$
Điều này xảy ra khi:
\(\left\{\begin{matrix} 3m>0\\ \Delta'=(2m-1)^2-3m(m-2)\leq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m>0\\ (m+1)^2\leq 0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} m>0\\ m=-1\end{matrix}\right.\) (vô lý)
Vậy không tồn tại $m$ để hs đồng biến trên $\mathbb{R}$

c: \(12\cdot3^x+3\cdot15^x-5^{x+1}=20\)
=>\(12\cdot3^x+3\cdot3^x\cdot5^x-5^x\cdot5-20=0\)
=>\(3^x\cdot3\left(5^x+4\right)-5\left(5^x+4\right)=0\)
=>\(\left(3^{x+1}-5\right)\left(5^x+4\right)=0\)
=>\(3^{x+1}-5=0\)
=>\(3^{x+1}=5\)
=>\(x+1=log_35\)
=>\(x=log_35-1\)
f: \(25^x-2\left(3-x\right)\cdot5^x+2x-7=0\)
=>\(\left(5^x\right)^2+5^x\cdot\left(2x-6\right)+2x-7=0\)
=>\(\left(5^x\right)^2+5^x\left(2x-7\right)+5^x+2x-7=0\)
=>\(5^x\left(5^x+2x-7\right)+\left(5^x+2x-7\right)=0\)
=>\(\left(5^x+1\right)\left(5^x+2x-7\right)=0\)
=>\(5^x+2x-7=0\)
Đặt \(A\left(x\right)=5^x+2x-7\)
=>\(A'\left(x\right)=5^x\cdot ln5+2>0\forall x\)
=>A(x) đồng biến trên R
=>A(x)=0 khi và chỉ khi x=1
i: \(9^x+2\left(x-2\right)\cdot3^x+2x-5=0\)
=>\(\left(3^x\right)^2+3^x\left(2x-5\right)+3^x+2x-5=0\)
=>\(\left(3^x+2x-5\right)\left(3^x+1\right)=0\)
=>\(3^x+2x-5=0\)
Đặt \(B\left(x\right)=3^x+2x-5\)
=>\(B'\left(x\right)=3^x\cdot ln3+2>0\)
=>B(x) luôn đồng biến trên R
=>B(x)=0 khi và chỉ khi x=1

Ta có: \(\int\dfrac{xdx}{x^2+3}\)
Đặt \(u=x^2+3\left(u>0\right)\)
Có \(du=2xdx\)
\(\Rightarrow\int\dfrac{xdx}{x^2+3}=\)\(\int\dfrac{du}{2u}=\dfrac{1}{2}ln\left(u\right)=\dfrac{1}{2}ln\left(x^2+3\right)\)

Lời giải:
\(\lim\limits_{x\to 2-}y=\lim\limits_{x\to 2-}\frac{\sqrt{4-x^2}}{(x-2)(x-3)}=\lim\limits_{x\to 2-}\frac{\sqrt{2+x}}{\sqrt{2-x}(x-3)}=-\infty \) nên $x=2$ là TCĐ
Vì \(x\in [-2;2)\) nên không tồn tại \(\lim\limits_{x\to +\infty }y\) nên đths không có TCN
Còn $x=3$ không thể là TCĐ vì tại $x=3$ thì $\sqrt{4-x^2}$ không tồn tại .

Gọi G là trọng tâm tam giác ABC
\(\overrightarrow{A'A}+\overrightarrow{B'B}+\overrightarrow{C'C}=\overrightarrow{0}\Leftrightarrow\overrightarrow{A'G}+\overrightarrow{GA}+\overrightarrow{B'G}+\overrightarrow{GB}+\overrightarrow{C'G}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{GA'}+\overrightarrow{GB'}+\overrightarrow{GC'}=\overrightarrow{0}\)
Goi G la trong tam tam giac A'B'C'
Lai co: \(\overrightarrow{G'A'}+\overrightarrow{G'B'}+\overrightarrow{G'C'}=\overrightarrow{0}\)
\(\Rightarrow G'\equiv G\Rightarrow G'=\left(1;0;-2\right)\)






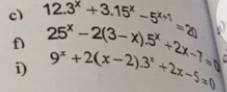


Câu 5: Thể tích của khối chóp đã cho: V = 1/3.2a2.2a = 4/3.a3. Chọn C.
Câu 6: Thể tích của khối chóp đã cho: V = 1/3.32.2 = 6. Chọn A.
Câu 7: Thể tích của khối chóp S.ABC: V = 1/3.1/2.a2.h = 5a3 ⇒ h = 30a. Chọn B.