
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a. Áp dụng hệ thức lượng trong tam giác vuông ta có:
$AH^2=BH.CH=4.6=24$
$\Rightarrow AH=\sqrt{24}=2\sqrt{6}$ (cm)
$AB^2=BH.BC=BH(BH+CH)=4(4+6)=40$
$\Rightarrow AB=\sqrt{40}=2\sqrt{10}$ (cm)
b.
$AC^2=CH.BC=6(6+4)=60$
$\Rightarrow AC=\sqrt{60}=2\sqrt{15}$ (cm)
$AM=AC:2=\sqrt{15}$ (cm)
$\tan \widehat{AMB}=\frac{AB}{AM}=\frac{2\sqrt{10}}{\sqrt{15}}=\frac{2\sqrt{6}}{3}$
$\Rightarrow \widehat{AMB}=59^0$
c.
Áp dụng hệ thức lượng trong tam giác vuông với tam giác $ABM$:
$BK.BM=AB^2(1)$
Áp dụng hệ thức lượng với tam giác $ABC$:
$AB^2=BH.BC(2)$
Từ $(1); (2)\Rightarrow BK.BM=BH.BC$


a: góc OBA+góc OCA=90+90=180 độ
=>ABOC nội tiếp
b: góc OIE=góc OCE=90 độ
=>OICE là tứ giác nội tiếp
=>góc OEI=góc OCI
=>góc OEI=góc OCB
OBAC nội tiếp
=>góc OCB=góc OAB
=>góc OEI=góc OAB
=>góc OEI=góc OAI
=>OIAE nội tiếp

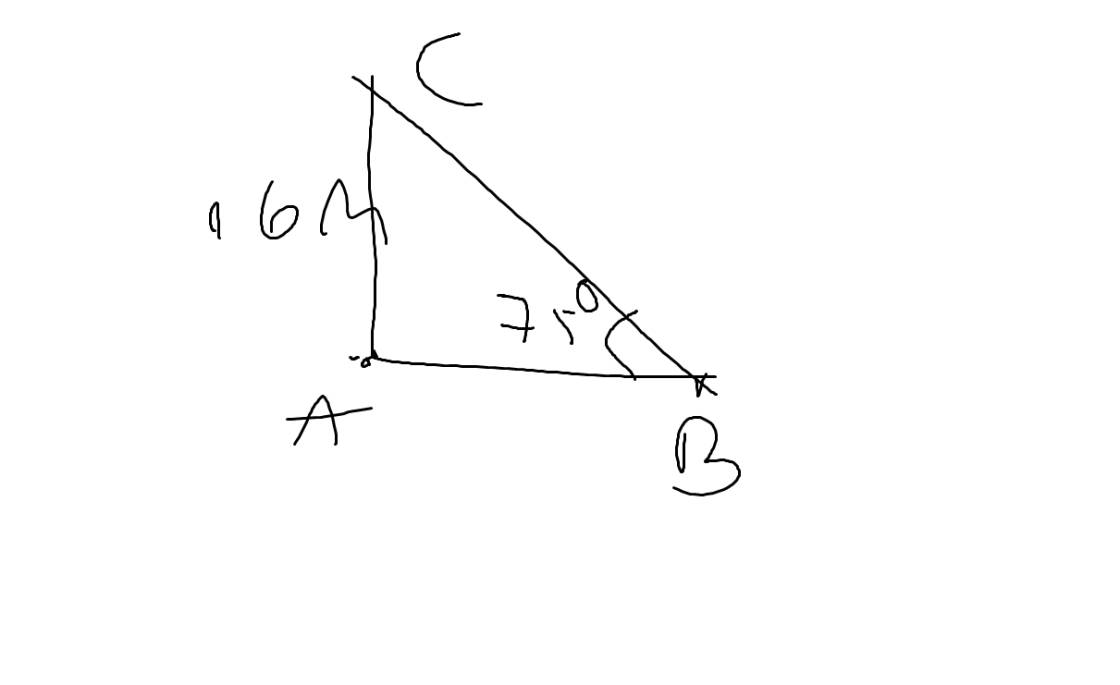
Gọi A,B lần lượt là hai mốc của bờ sông. Gọi điểm C là điểm nằm trên đường thước dây vuông góc với bờ sông tại A
=>AB vuông góc AC tại A
Theo đề, ta có: AC=16m \(\widehat{ABC}=75^0\)
Xét ΔABC vuông tại A có \(tanB=\dfrac{AC}{AB}\)
=>\(AB=\dfrac{AC}{tanB}=16:tan75\simeq4,3\left(m\right)\)

1) ĐKXĐ: \(x\ge0\)
2) ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne9\end{matrix}\right.\)
3) ĐKXĐ: \(x\ge4\)
4) ĐKXĐ: \(x>16\)
5) ĐKXĐ: \(\left[{}\begin{matrix}x\le-2\\x\ge0\end{matrix}\right.\)
6) ĐKXĐ: \(\left[{}\begin{matrix}x\le-1\\x\ge4\end{matrix}\right.\)
7) ĐKXĐ: \(\left[{}\begin{matrix}1\le x\\x< 3\end{matrix}\right.\)
8) ĐKXĐ: \(\left[{}\begin{matrix}x\le-2\\x>3\end{matrix}\right.\)
9) ĐKXĐ: \(x\in R\)
10) ĐKXĐ: \(x\in R\)
11) ĐKXĐ: \(x\in R\)
12) ĐKXĐ: \(x\in R\)
13) ĐKXĐ: \(x\in R\)
14) ĐKXĐ: \(x\in R\)
15) ĐKXĐ: \(x\in R\)
16) ĐKXĐ: \(x\ne-\dfrac{1}{2}\)
17) ĐKXĐ: \(x\ge7\)
18) ĐKXĐ: \(x\ge-5\)

Đài ơi, giải giúp cho Sarah đi, tớ không có viết và giờ vào giường rồi , good nigh

Câu 10:
Gọi \(H\) là giao điểm của \(MO\) và \(AB\).
Xét tam giác \(MAO\) vuông tại \(A\) đường cao \(AH\):
\(\dfrac{1}{AH^2}=\dfrac{1}{MA^2}+\dfrac{1}{AO^2}\Leftrightarrow\dfrac{1}{\left(\dfrac{R\sqrt{2}}{2}\right)^2}=\dfrac{1}{MA^2}+\dfrac{1}{R^2}\Leftrightarrow MA=R\).
\(S_{MAOB}=S_{MAO}+S_{MBO}\)
\(=\dfrac{1}{2}.AO.MA+\dfrac{1}{2}.OB.MB\)
\(=\dfrac{1}{2}.R.R+\dfrac{1}{2}.R.R=R^2\)
Chọn C.

Bài `13`
\(a,\sqrt{27}+\sqrt{48}-\sqrt{108}-\sqrt{12}\\ =\sqrt{9\cdot3}+\sqrt{16\cdot3}-\sqrt{36\cdot3}-\sqrt{4\cdot3}\\ =3\sqrt{3}+4\sqrt{3}-6\sqrt{3}-2\sqrt{3}\\ =\left(3+4-6-2\right)\sqrt{3}\\ =-\sqrt{3}\\ b,\left(\sqrt{28}+\sqrt{12}-\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{84}\\ =\left(\sqrt{4\cdot7}+\sqrt{4\cdot3}-\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{4\cdot21}\\ =\left(2\sqrt{7}+2\sqrt{3}-\sqrt{7}\right)\cdot\sqrt{7}+2\sqrt{21}\\ =2\cdot7+2\sqrt{21}-7+2\sqrt{21}\\ =14+2\sqrt{21}-7+2\sqrt{21}\\ =7+4\sqrt{21}\)

Bài 2:
a: \(\text{Δ}=\left(-2\right)^2-4\left(m-3\right)=4-4m+12=-4m+16\)
Để pt vô nghiệm thì -4m+16<0
=>m>4
Để phương trình co nghiệmduy nhất thì -4m+16=0
=>m=4
Để phương trình có hai nghiệm phân biệt thì -4m+16>0
=>m<4
b: \(\text{Δ}=\left(2m-2\right)^2-4\left(m^2-m+1\right)\)
\(=4m^2-8m+4-4m^2+4m-4=-4m\)
Để pt vô nghiệm thì -4m<0
=>m>0
Để phương trình co nghiệmduy nhất thì -4m=0
=>m=0
Để phương trình có hai nghiệm phân biệt thì -4m>0
=>m<0
c: \(\Delta=\left(-m\right)^2-4\cdot1\cdot1=m^2-4\)
Để pt vô nghiệm thì m^2-4<0
=>-2<m<2
Để phương trình co nghiệmduy nhất thì m^2-4=0
=>m=2 hoặc m=-2
Để phương trình có hai nghiệm phân biệt thì m^2-4>0
=>m>2 hoặc m<-2


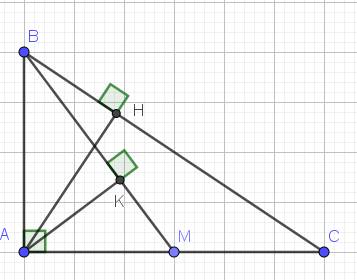
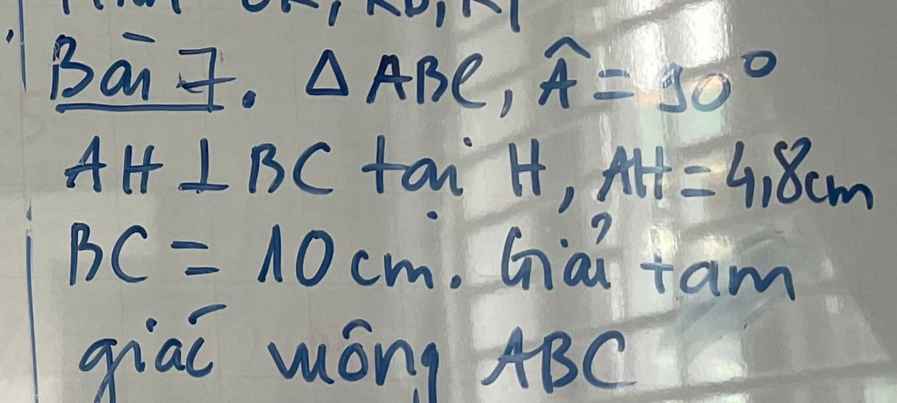







 em cần giải gấp bài 2 ạ, mọi người giúp em với ạ
em cần giải gấp bài 2 ạ, mọi người giúp em với ạ
Gọi tuổi An hiện nay là \(x\) (tuổi; \(x\) \(\in\) N*).
Khi tuổi cô Hoa gấp ba lần tuổi An hiện nay thì tuổi cô Hoa khi đó là:
3.\(x\) (tuổi)
Tuổi An khi đó là: 3\(x\) - 22 (tuổi)
Theo bài ra ta có phương trình:
3\(x\) = (3\(x\) - 22). 12
3\(x\) = 36\(x\) - 264
36\(x\) - 3\(x\) = 264
33\(x\) = 264
\(x\) = 264 : 33
\(x\) = 8
Tuổi An hiện nay là: 8 tuổi
Tuổi cô Hoa hiện nay là: 8 + 22 = 30 (tuổi)
Kết luận:...