
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
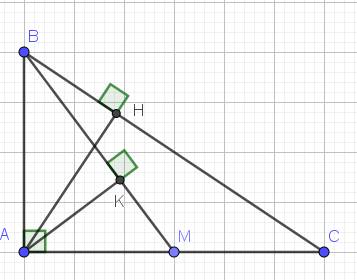
a. Áp dụng hệ thức lượng trong tam giác vuông ta có:
$AH^2=BH.CH=4.6=24$
$\Rightarrow AH=\sqrt{24}=2\sqrt{6}$ (cm)
$AB^2=BH.BC=BH(BH+CH)=4(4+6)=40$
$\Rightarrow AB=\sqrt{40}=2\sqrt{10}$ (cm)
b.
$AC^2=CH.BC=6(6+4)=60$
$\Rightarrow AC=\sqrt{60}=2\sqrt{15}$ (cm)
$AM=AC:2=\sqrt{15}$ (cm)
$\tan \widehat{AMB}=\frac{AB}{AM}=\frac{2\sqrt{10}}{\sqrt{15}}=\frac{2\sqrt{6}}{3}$
$\Rightarrow \widehat{AMB}=59^0$
c.
Áp dụng hệ thức lượng trong tam giác vuông với tam giác $ABM$:
$BK.BM=AB^2(1)$
Áp dụng hệ thức lượng với tam giác $ABC$:
$AB^2=BH.BC(2)$
Từ $(1); (2)\Rightarrow BK.BM=BH.BC$


Đài ơi, giải giúp cho Sarah đi, tớ không có viết và giờ vào giường rồi , good nigh

Câu 10:
Gọi \(H\) là giao điểm của \(MO\) và \(AB\).
Xét tam giác \(MAO\) vuông tại \(A\) đường cao \(AH\):
\(\dfrac{1}{AH^2}=\dfrac{1}{MA^2}+\dfrac{1}{AO^2}\Leftrightarrow\dfrac{1}{\left(\dfrac{R\sqrt{2}}{2}\right)^2}=\dfrac{1}{MA^2}+\dfrac{1}{R^2}\Leftrightarrow MA=R\).
\(S_{MAOB}=S_{MAO}+S_{MBO}\)
\(=\dfrac{1}{2}.AO.MA+\dfrac{1}{2}.OB.MB\)
\(=\dfrac{1}{2}.R.R+\dfrac{1}{2}.R.R=R^2\)
Chọn C.

18) Ta có: \(H=\dfrac{x^2+\sqrt{x}}{x-\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}\)
\(=\sqrt{x}\cdot\left(\sqrt{x}+1\right)-\left(2\sqrt{x}-1\right)\)
\(=x+\sqrt{x}-2\sqrt{x}+1\)
\(=x-\sqrt{x}+1\)
19) Ta có: \(T=\dfrac{a-3\sqrt{a}-4}{\sqrt{a}+1}\)
\(=\dfrac{\left(\sqrt{a}-4\right)\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\)
\(=\sqrt{a}-4\)

a) \(\widehat{AED}=\widehat{AFD}=90^o\) nên \(E,F\) cùng nhìn \(AD\) dưới góc vuông suy ra \(AEDF\) nội tiếp.
suy ra \(\widehat{AEF}=\widehat{ADF}\).
mà \(\widehat{ADF}=\widehat{ACD}\) (vì cùng phụ với góc \(\widehat{DAC}\))
suy ra \(\widehat{AEF}=\widehat{ACD}\Rightarrow\widehat{BEF}+\widehat{FCB}=180^o\) suy ra \(BEFC\) nội tiếp.
b) \(\Delta GBE\sim\Delta GFC\left(g.g\right)\)
suy ra \(GB.GC=GE.GF\).
\(\Delta GDE\sim\Delta GFD\left(g.g\right)\)
suy ra \(GD^2=GE.GF\).
\(ACBH\) nội tiếp suy ra \(GB.GC=GH.GA\)
suy ra \(GD^2=GH.GA\)
\(\Rightarrow\Delta GHD\sim\Delta GDA\left(c.g.c\right)\)
\(\Rightarrow\widehat{GHD}=\widehat{GDA}=90^o\)
suy ra \(DH\) vuông góc với \(AG\).

Bài `13`
\(a,\sqrt{27}+\sqrt{48}-\sqrt{108}-\sqrt{12}\\ =\sqrt{9\cdot3}+\sqrt{16\cdot3}-\sqrt{36\cdot3}-\sqrt{4\cdot3}\\ =3\sqrt{3}+4\sqrt{3}-6\sqrt{3}-2\sqrt{3}\\ =\left(3+4-6-2\right)\sqrt{3}\\ =-\sqrt{3}\\ b,\left(\sqrt{28}+\sqrt{12}-\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{84}\\ =\left(\sqrt{4\cdot7}+\sqrt{4\cdot3}-\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{4\cdot21}\\ =\left(2\sqrt{7}+2\sqrt{3}-\sqrt{7}\right)\cdot\sqrt{7}+2\sqrt{21}\\ =2\cdot7+2\sqrt{21}-7+2\sqrt{21}\\ =14+2\sqrt{21}-7+2\sqrt{21}\\ =7+4\sqrt{21}\)
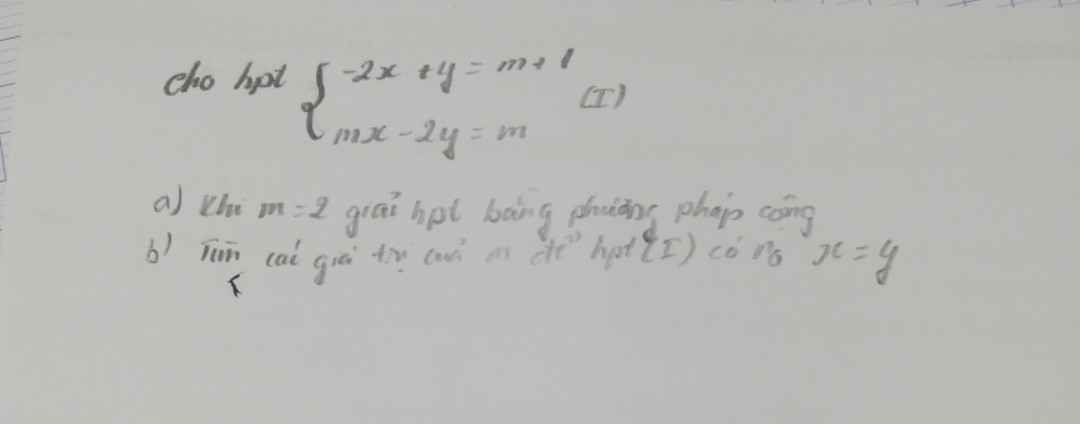 Giải giúp em với ạ,em cảm ơn
Giải giúp em với ạ,em cảm ơn
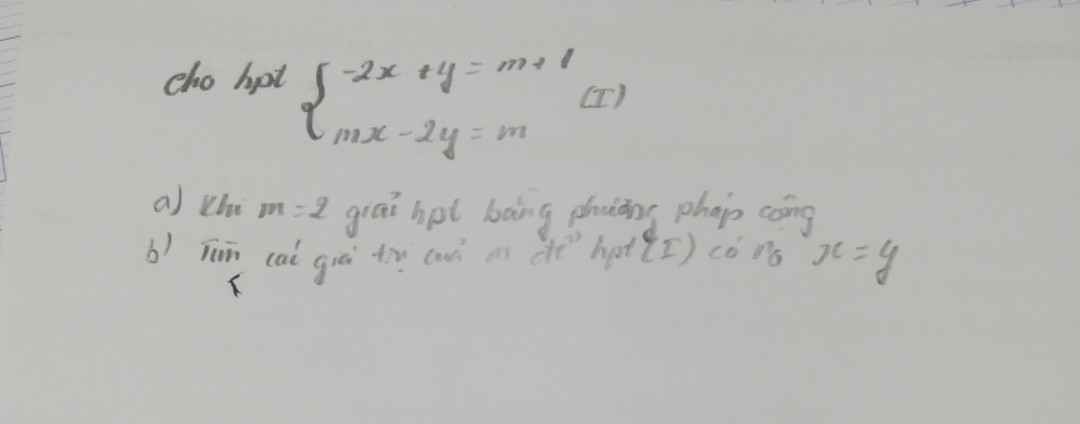 Giải giúp em với ạ,em cảm ơn
Giải giúp em với ạ,em cảm ơn

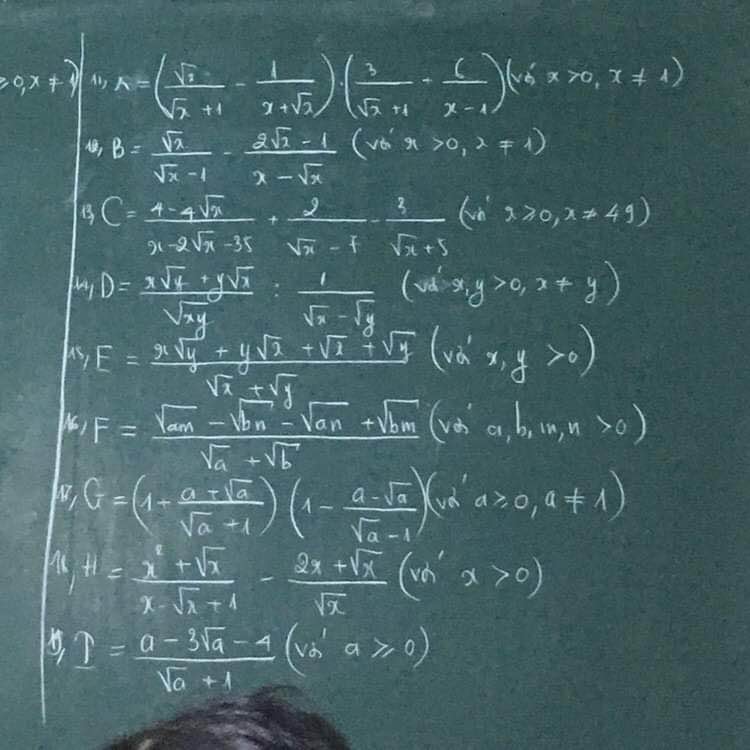
 Giúp em giải bài tập này với ạ. Em cảm ơn.
Giúp em giải bài tập này với ạ. Em cảm ơn.