
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: \(\sqrt{\dfrac{1}{200}}=\dfrac{\sqrt{2}}{20}\)
2: \(\dfrac{5}{1-\sqrt{6}}=-1-\sqrt{6}\)
3: \(\dfrac{1}{1-\sqrt{2}}-\dfrac{1}{1+\sqrt{2}}\)
\(=\dfrac{1+\sqrt{2}-1+\sqrt{2}}{-1}\)
\(=-2\sqrt{2}\)

2: Ta có: \(\sqrt{16-6\sqrt{7}}\cdot\left(3+\sqrt{7}\right)\)
\(=\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)\)
=9-7
=2
3: Ta có: \(\left(\sqrt{6}+\sqrt{14}\right)\cdot\sqrt{5-2\sqrt{21}}\)
\(=\left(\sqrt{7}+\sqrt{3}\right)\left(\sqrt{7}-\sqrt{3}\right)\)
=7-3
=4
\(1,=\sqrt{\left(5+2\sqrt{6}\right)^2}-\sqrt{\left(3-\sqrt{6}\right)^2}=5+2\sqrt{6}-3+\sqrt{6}=2+3\sqrt{6}\\ 2,=\sqrt{\left(3-\sqrt{7}\right)^2}\left(3+\sqrt{7}\right)=\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)=9-7=2\\ 3,=\left(\sqrt{3}+\sqrt{7}\right)\sqrt{10-2\sqrt{21}}=\left(\sqrt{3}+\sqrt{7}\right)\sqrt{\left(\sqrt{7}-\sqrt{3}\right)^2}\\ =\left(\sqrt{7}+\sqrt{3}\right)\left(\sqrt{7}-\sqrt{3}\right)=7-3=4\\ 4,=\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{6+2\sqrt{5}}+\sqrt{4-2\sqrt{3}}\right)\\ =\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+1+\sqrt{3}-1\right)\\ =\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)=5-3=2\)
\(5,\\ =\sqrt{\left(3\sqrt{3}-5\right)^2}+\sqrt{\left(5-2\sqrt{3}\right)^2}=3\sqrt{3}-5+5-2\sqrt{3}=\sqrt{3}\\ 6,=\sqrt{13-4\sqrt{10}}-\sqrt{53+12\sqrt{10}}\\ =\sqrt{\left(2\sqrt{2}-\sqrt{5}\right)^2}-\sqrt{\left(3\sqrt{5}-2\sqrt{2}\right)^2}\\ =2\sqrt{2}-\sqrt{5}-3\sqrt{5}+2\sqrt{2}=4\sqrt{2}-4\sqrt{5}\)

Áp dụng tslg của góc nhọn trong tam giác ABH vuông tại H:
\(sinB=\dfrac{AH}{AB},cosB=\dfrac{BH}{AB},tanB=\dfrac{AH}{BH},cotB=\dfrac{BH}{AH}\)
Áp dụng tslg của góc nhọn trong tam giác AHC vuông tại H :
\(sinC=\dfrac{AH}{AC},cosC=\dfrac{HC}{AC},tanC=\dfrac{AH}{HC},cotC=\dfrac{HC}{AH}\)
\(\sin B=\dfrac{AH}{AB};\cos B=\dfrac{BH}{AB};\tan B=\dfrac{AH}{BH};\cot B=\dfrac{BH}{AH}\\ \sin C=\dfrac{AH}{AC};\cos C=\dfrac{CH}{AC};\tan C=\dfrac{AH}{HC};\cot C=\dfrac{HC}{AH}\)

\(\tan B=\dfrac{AC}{AB}=\dfrac{5}{12}\Rightarrow AC=\dfrac{5\cdot6}{12}=2,5\left(cm\right)\\ BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+2,5^2}=6,5\left(cm\right)\)
Áp dụng tslg của góc nhọn trong tam giác ABC vuông tại A:
\(tanB=\dfrac{AC}{AB}=\dfrac{5}{12}\)
\(\Rightarrow\dfrac{AC}{6}=\dfrac{5}{12}\Rightarrow AC=2,5\left(cm\right)\)
Xét tam giác ABC vuông tại A có:
\(BC^2=AB^2+AC^2\left(Pytago\right)\)
\(\Rightarrow BC^2=6^2+\left(2,5\right)^2=42,25\Rightarrow BC=6,5\left(cm\right)\)



Ta có: \(sin^2\alpha+cos^2\alpha=1\)
\(\Rightarrow sin\alpha=\sqrt{1-cos^2\alpha}=\sqrt{1-\left(\dfrac{\sqrt{3}}{2}\right)^2}=\dfrac{1}{2}\)
Ta có: \(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{1}{2}:\dfrac{\sqrt{3}}{2}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}\)
Ta có: \(tan\alpha.cot\alpha=1\)
\(\Rightarrow cot\alpha=\dfrac{1}{tan\alpha}=1:\dfrac{\sqrt{3}}{3}=\dfrac{3}{\sqrt{3}}=\sqrt{3}\)



\(a,\sin^243^0+\sin^244^0+\sin^245^0+\sin^246^0+\sin^247^0\\ =\cos^247^0+\cos^246^0+\sin^245^0+\sin^246^0+\sin^247^0\\ =\left(\cos^247^0+\sin^247^0\right)+\left(\cos^246^0+\sin^246^0\right)+\sin^245^0=1+1+0,5=2,5\)
\(b,=\sin^289^0+\sin^288^0+...+\sin^246^0+\cos^245^0+\cos^246^0+...+\cos^288^0+\cos^289^0\\ =\left(\sin^289^0+\cos^289^0\right)+\left(\sin^288^0+\cos^288^0\right)+...+\left(\sin^246^0+\cos^246^0\right)+\cos^245^0\\ =1+1+..+1+0,5=44,5\)
\(c,=2\sqrt{\dfrac{\cot68^0}{\cot68^0}}+\cot34^0\cdot\cot56^0=2+1=3\)

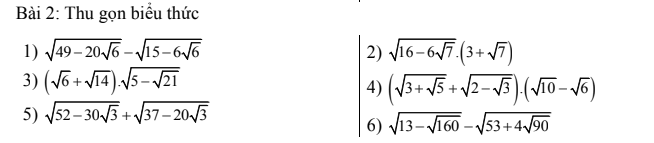

a: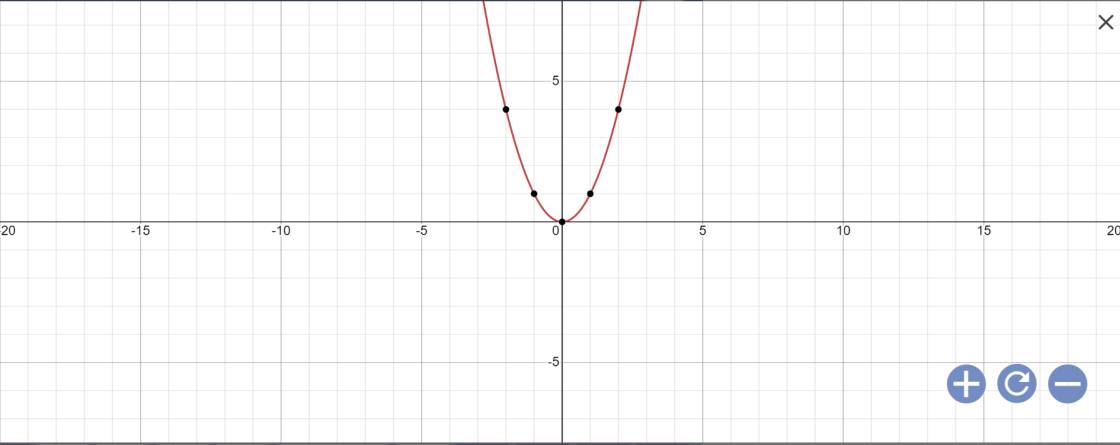
b: Phương trình hoành độ giao điểm là:
\(x^2=\left(m-2\right)x+6\)
=>\(x^2-\left(m-2\right)x-6=0\)
\(a\cdot c=1\cdot\left(-6\right)=-6< 0\)
=>(P) luôn cắt (d) tại hai điểm phân biệt
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=m-2\\x_1x_2=\dfrac{c}{a}=-6\end{matrix}\right.\)
\(x_2^2-x_1x_2+\left(m-2\right)x_1=16\)
=>\(x_2^2+x_1\left(x_1+x_2\right)-x_1x_2=16\)
=>\(x_2^2+x_1^2=16\)
=>\(\left(x_1+x_2\right)^2-2x_1x_2=16\)
=>\(\left(m-2\right)^2-2\cdot\left(-6\right)=16\)
=>\(\left(m-2\right)^2=4\)
=>\(\left[{}\begin{matrix}m-2=2\\m-2=-2\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}m=4\\m=0\end{matrix}\right.\)