
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 3:
a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)
b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)
nên BC<AC=AB
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
Câu 2
a) Thay y = -2 vào biểu thức đã cho ta được:
2.(-2) + 3 = -1
Vậy giá trị của biểu thức đã cho tại y = -2 là -1
b) Thay x = -5 vào biểu thức đã cho ta được:
2.[(-5)² - 5] = 2.(25 - 5) = 2.20 = 40
Vậy giá trị của biểu thức đã cho tại x = -5 là 40

Hình 1:
a: Ta có: AC//BD
AB\(\perp\)AC
Do đó: BD\(\perp\)AB

Đặt : \(\dfrac{x}{5}=\dfrac{y}{3}=k\)
`=>x=5k,y=3k`
Ta có : \(x^2-y^2=4=>\left(5k\right)^2-\left(3k\right)^2=4\\ =>25k^2-9k^2=4\\ =>16k^2=4\\ =>k^2=\dfrac{1}{4}\\ =>k=\pm\dfrac{1}{2}\)
\(=>\left[{}\begin{matrix}\left\{{}\begin{matrix}x=\dfrac{5}{2}\\y=\dfrac{3}{2}\end{matrix}\right.\\\left\{{}\begin{matrix}x=-\dfrac{5}{2}\\y=-\dfrac{3}{2}\end{matrix}\right.\end{matrix}\right.\)

Từ giả thiết, suy ra: \(\hat{M}=\dfrac{3}{2}\hat{P}\).
Ta có: \(\hat{D}+\hat{M}+\hat{P}=180^o\) (tổng 3 góc trong một tam giác)
\(\Leftrightarrow55^o+\dfrac{3}{2}\hat{P}+\hat{P}=180^o\Leftrightarrow\hat{P}=50^o\)
\(\Rightarrow\hat{M}=\dfrac{3}{2}\hat{P}=\dfrac{3}{2}\cdot50^o=75^o\)

\(=4\)
Cái này thì bạn rút gọn x - 1 thì còn \(\dfrac{-12}{-3}\)
Sau đó rút gọn -12 và -3 thì chỉ còn 4 thôi
=>(x-1)2 = -12 . (-3)
(x-1)2 = 36
(x-1)2 = 62 = (-6)2
*) x-1=6 *) x-1=-6
x=7 x=-5
=>x thuộc (7,-5)


Bài 1
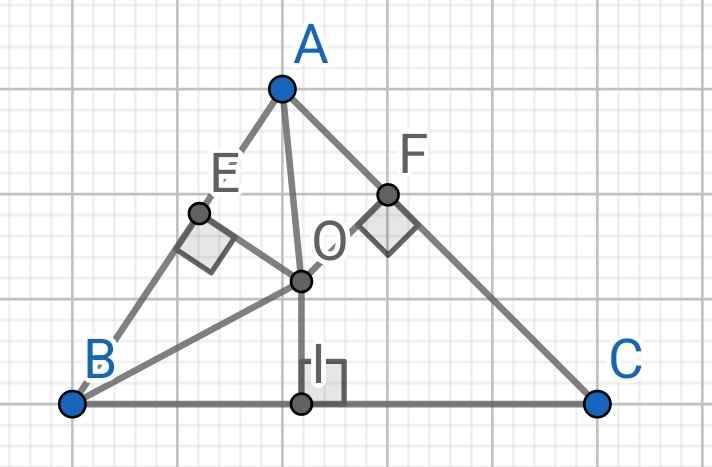 Do BO là tia phân giác của ∠ABC (gt)
Do BO là tia phân giác của ∠ABC (gt)
⇒ ∠OBE = ∠OBI
Do AO là tia phân giác của ∠BAC (gt)
⇒ ∠OAE = ∠OAF
Xét hai tam giác vuông: ∆OAE và ∆OAF có:
OA chung
∠OAE = ∠OAF (cmt)
⇒ ∆OAE = ∆OAF (cạnh huyền - góc nhọn)
⇒ OE = OF (hai cạnh tương ứng) (1)
Xét hai tam giác vuông: ∆OBE và ∆OBI có:
OB chung
∠OBE = ∠OBI (cmt)
⇒ ∆OBE = ∆OBI (cạnh huyền - góc nhọn)
⇒ OE = OI (hai cạnh tương ứng) (2)
Từ (1) và (2) ⇒ OE = OF = OI
Bài 2
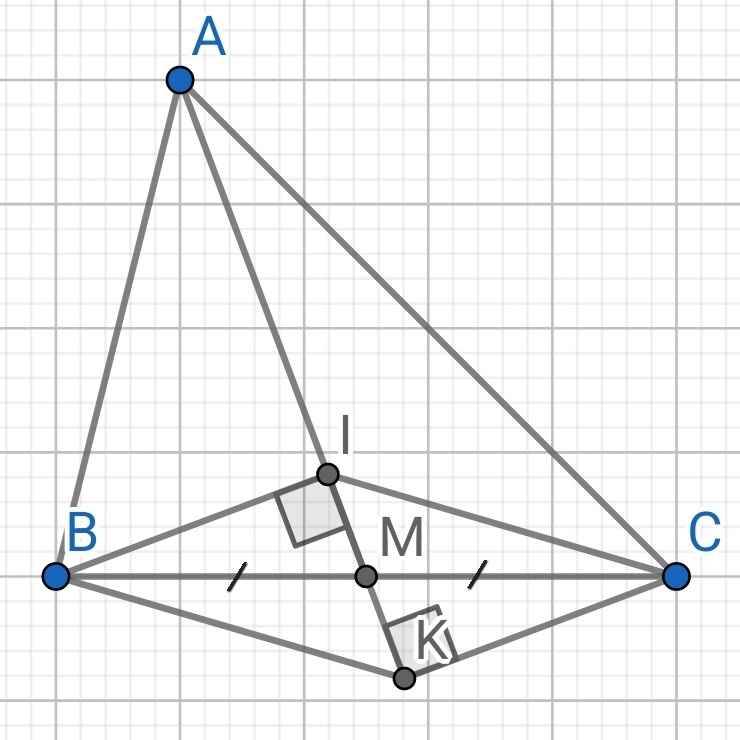 a) Xét hai tam giác vuông: ∆BMI và ∆CMK có:
a) Xét hai tam giác vuông: ∆BMI và ∆CMK có:
BM = CM (gt)
∠BMI = ∠CMK (đối đỉnh)
⇒ ∆BMI = ∆CMK (cạnh huyền - góc nhọn)
⇒ BI = CK (hai canhk tương ứn
b) Do ∆BMI = ∆CMK (cmt)
⇒ MI = MK (hai cạnh tương ứng)
Xét ∆BMK và ∆CMI có:
MK = MI (cmt)
∠BMK = ∠CMI (đối đỉnh)
BM = CM (gt)
⇒ ∆BMK = ∆CMI (c-g-c)
⇒ ∠MBK = ∠MCI (hai góc tương ứng)
Mà ∠MBK và ∠MCI là hai góc so le trong)
⇒ BK // CI

3:
a: Xét ΔACE vuông tại C và ΔAKE vuông tại K có
AE chung
góc CAE=góc KAE
=>ΔACE=ΔAKE
=>AC=AK và EC=EK
=>AE là trung trực của CK
=>AE vuông góc CK
b: Xét ΔEAB có góc EAB=góc EBA
nên ΔEAB cân tại E
mà EK là đường cao
nên KA=KB
c: EB=EA
EA>AC
=>EB>AC
d: Gọi giao của BD và AC là M
Xét ΔAMB có
AD,BC là đường cao
AD cắt BC tại E
=>E là trực tâm
=>ME vuông góc BC
=>M,E,K thẳng hàng
=>ĐPCM


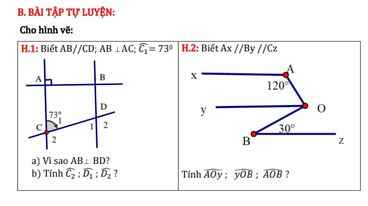 giúp mik giải bài toán hình 7 này với ạ
giúp mik giải bài toán hình 7 này với ạ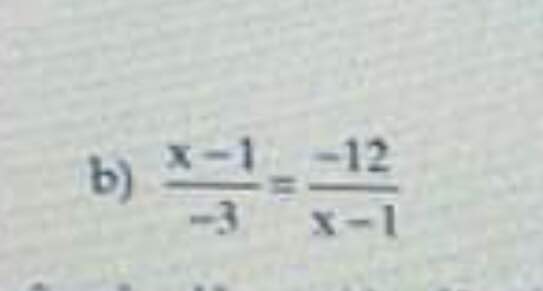



b: Xét tứ giác ABCK có
M là trung điểm của AC
M là trung điểm của BK
Do đó: ABCK là hình bình hành
Suy ra: BC=AK