
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\overline{abcd}\)
a có 1 cách chọn
d có 5 cách chọn
b có 8 cách chọn
c có 7 cách chọn
=>Có 5*8*7=280 cách

a. Ta có : \(SA\perp\left(ABCD\right)\Rightarrow BC\perp SA\)
Đáy ABCD là HV \(\Rightarrow BC\perp AB\)
Suy ra : \(BC\perp\left(SAB\right)\Rightarrow\left(SAB\right)\perp\left(SBC\right)\) ( đpcm )
b. \(\left(SBD\right)\cap\left(ABCD\right)=BD\)
O = \(AC\cap BD\) ; ta có : \(AO\perp BD;AO=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{2}a\)
Dễ dàng c/m : \(BD\perp\left(SAC\right)\) \(\Rightarrow SO\perp BD\)
Suy ra : \(\left(\left(SBD\right);\left(ABCD\right)\right)=\left(SO;AO\right)=\widehat{SOA}\)
\(\Delta SAO\perp\) tại A có : tan \(\widehat{SOA}=\dfrac{SA}{AO}=\dfrac{a}{\dfrac{\sqrt{2}}{2}a}=\sqrt{2}\)
\(\Rightarrow\widehat{SOA}\approx54,7^o\) \(\Rightarrow\) ...

12.
\(y=\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\le\sqrt[]{2}\)
\(\Rightarrow M=\sqrt{2}\)
13.
Pt có nghiệm khi:
\(5^2+m^2\ge\left(m+1\right)^2\)
\(\Leftrightarrow2m\le24\)
\(\Rightarrow m\le12\)
14.
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=-\dfrac{5}{3}\left(loại\right)\end{matrix}\right.\)
\(\Leftrightarrow x=k2\pi\)
15.
\(\Leftrightarrow\left[{}\begin{matrix}tanx=-1\\tanx=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=arctan\left(3\right)+k\pi\end{matrix}\right.\)
Đáp án A
16.
\(\dfrac{\sqrt{3}}{2}sinx-\dfrac{1}{2}cosx=\dfrac{1}{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{6}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{6}=\dfrac{\pi}{6}+k2\pi\\x-\dfrac{\pi}{6}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)
\(\left[{}\begin{matrix}2\pi\le\dfrac{\pi}{3}+k2\pi\le2018\pi\\2\pi\le\pi+k2\pi\le2018\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}1\le k\le1008\\1\le k\le1008\end{matrix}\right.\)
Có \(1008+1008=2016\) nghiệm

Bạn đọc thử xem và tham khảo nhé, nếu sai hay không hiểu thì cứ nói mình nha

Ta có tổng hệ số của khai triển (a+b)^n là Cn0+C1n+....Cnn
theo đề ta có Cn0+C1n+....Cnn=4096=>(1+1)^n=4096=>2^n=4096=>n=12
vậy n=12
Xét Ck12>Ck+112=>k<11/2=>k=1,2,3,4,5
=>C112<C212<...<C512<C612>C712>.......>C1212
vậy k max =6=> hệ số lớn nhất trong khai triển:C126=924=>A





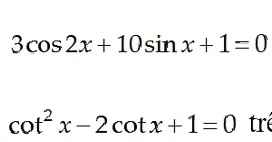



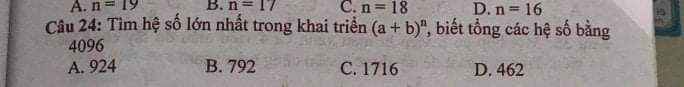
Trong mp đáy, qua B kẻ đường thẳng song song AC, lần lượt cắt DA và DC kéo dài tại E và F
\(\Rightarrow AC||\left(SEF\right)\Rightarrow d\left(AC;SB\right)=d\left(AC;\left(SEF\right)\right)=d\left(A;\left(SEF\right)\right)\)
Gọi I là giao điểm AC và BD
Theo định lý Talet: \(\dfrac{ID}{IB}=\dfrac{DC}{AB}=3\Rightarrow\dfrac{ID}{BD}=\dfrac{3}{4}\)
Cũng theo Talet: \(\dfrac{DA}{DE}=\dfrac{DI}{DB}=\dfrac{3}{4}\Rightarrow AD=\dfrac{3}{4}DE\Rightarrow AE=\dfrac{1}{4}DE\)
\(\Rightarrow d\left(A;\left(SEF\right)\right)=\dfrac{1}{4}d\left(D;\left(SEF\right)\right)\)
Trong tam giác vuông EDF, kẻ \(DH\perp EF\) , trong tam giác vuông SDH, kẻ \(DK\perp SH\)
\(\Rightarrow DK\perp\left(SEF\right)\Rightarrow DK=d\left(D;\left(SEF\right)\right)\)
\(DE=\dfrac{4}{3}AD=\dfrac{4a}{3}\); \(DF=\dfrac{4}{3}DC=4a\)
\(\dfrac{1}{DH^2}=\dfrac{1}{DE^2}+\dfrac{1}{DF^2}=\dfrac{5}{8a^2}\)
\(\dfrac{1}{DK^2}=\dfrac{1}{SD^2}+\dfrac{1}{DH^2}=\dfrac{1}{48a^2}+\dfrac{5}{8a^2}\Rightarrow DK=\dfrac{4a\sqrt{93}}{31}\)
\(\Rightarrow d\left(AC;SB\right)=\dfrac{1}{4}DK=\dfrac{a\sqrt{93}}{31}\)