
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(g'\left(x\right)=\left(-2x\right)'\cdot f'\left(-2x\right)\)
\(=-2\cdot f'\left(-2x\right)\)
\(=-2\left(-2x^2-4x\right)\)
\(=4x^2+8x\)
\(g''\left(x\right)=4\cdot2x+8=8x+8\)
g'(x)=0
=>4x(x+2)=0
=>x=0 hoặc x=-2
Khi x=0 thì \(g''\left(x\right)=8\cdot0+8=8\)>0
=>Khi x=0 thì g(x) đạt giá trị cực đại
Khi x=-2 thì \(g''\left(x\right)=8\cdot\left(-2\right)+8=-8< 0\)
=>Khi x=-2 thì g(x) không đạt giá trị cực đại
Vậy: G(x) đạt giá trị cực đại tại x=0

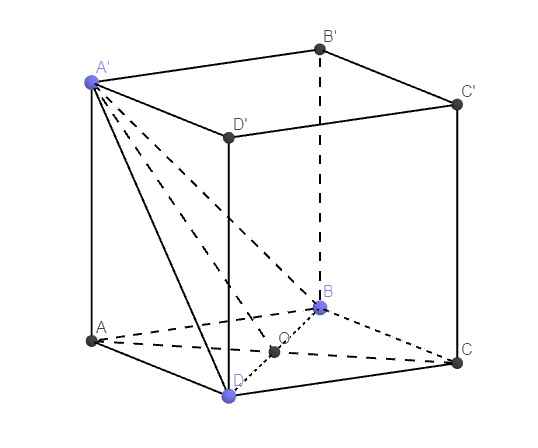
44.
\(AB=\dfrac{BD}{\sqrt{2}}=2a\sqrt{2}\)
Gọi O là giao điểm AC và BD \(\Rightarrow AO\perp BD\Rightarrow BD\perp\left(A'AO\right)\)
\(\Rightarrow\widehat{A'OA}\) là góc giữa (A'BD) và (ABCD)
\(\Rightarrow\widehat{A'OA}=60^0\)
\(\Rightarrow A'A=AO.tan60^0=\dfrac{BD}{2}.tan60^0=2a\sqrt{3}\)
\(\Rightarrow V=A'A.AB^2=16\sqrt{3}a^3\)



Không ai vẽ hình khi làm bài mặt cầu Oxyz đâu bạn, chỉ cần đại số hóa nó là được.
Gọi I là tâm mặt cầu, do mặt cầu tiếp xúc (Q) tại H nên \(IH\perp\left(Q\right)\)
\(\Rightarrow\) Đường thẳng IH nhận vtpt của (Q) là 1 vtcp
\(\Rightarrow\) IH nhận (1;1;-1) là 1 vtcp
Phương trình IH: \(\left\{{}\begin{matrix}x=1+t\\y=-1+t\\z=-t\end{matrix}\right.\)
I vừa thuộc IH vừa thuộc (P) nên là giao điểm của IH và (P)
\(\Rightarrow\) Tọa độ I thỏa mãn:
\(2\left(1+t\right)+\left(-1+t\right)+\left(-t\right)-3=0\)
\(\Rightarrow t=1\Rightarrow I\left(2;0;-1\right)\)
\(\Rightarrow\overrightarrow{IH}=\left(-1;-1;1\right)\Rightarrow R=IH=\sqrt{3}\)
Phương trình (S):
\(\left(x-2\right)^2+y^2+\left(z+1\right)^2=3\)

31/
\(3z^2-2z+27=0\)
\(\Delta'=\left(-1\right)^2-3.27=1-3.27=-80\)
\(\Delta'\) có 2 căn bậc 2 là \(\pm4i\sqrt{5}\)
\(\Rightarrow\left\{{}\begin{matrix}z_1=\dfrac{1+4i\sqrt{5}}{3}\\z_2=\dfrac{1-4i\sqrt{5}}{3}\end{matrix}\right.\Rightarrow\left|z_1\right|=\left|z_2\right|=\sqrt{\left(\dfrac{1}{3}\right)^2+\left(\dfrac{4\sqrt{5}}{3}\right)^2}=3\)
\(\Rightarrow z_1\left|z_2\right|+z_2\left|z_1\right|=1+4i\sqrt{5}+1-4i\sqrt{5}=2\) => A
32/ \(\Delta'=4-29=-25\Rightarrow\left\{{}\begin{matrix}z_1=-2+5i\\z_2=-2-5i\end{matrix}\right.\Rightarrow\left|z_1\right|=\left|z_2\right|=\sqrt{2^2+5^2}=\sqrt{29}\)
\(\Rightarrow\left|z_1\right|^4+\left|z_2\right|^4=2.\sqrt{29^4}=1682\) => B
33/ \(\Delta=1-12=-11\Rightarrow\left\{{}\begin{matrix}z_1=\dfrac{1+i\sqrt{11}}{6}\\z_2=\dfrac{1-i\sqrt{11}}{6}\end{matrix}\right.\Rightarrow\left|z_1\right|=\left|z_2\right|=\sqrt{\left(\dfrac{1}{6}\right)^2+\left(\dfrac{\sqrt{11}}{6}\right)^2}=\dfrac{\sqrt{3}}{3}\)
\(\Rightarrow\left|z_1\right|+\left|z_2\right|=\dfrac{2\sqrt{3}}{3}\) => D
34/ \(\Delta=1-4.3.2=-23\Rightarrow\left\{{}\begin{matrix}z_1=\dfrac{1-i\sqrt{23}}{6}\\z_2=\dfrac{1+i\sqrt{23}}{6}\end{matrix}\right.\Rightarrow\left|z_1\right|=\left|z_2\right|=\sqrt{\dfrac{1}{36}+\dfrac{23}{36}}=\dfrac{\sqrt{6}}{3}\)
\(\Rightarrow T=2.\left(\dfrac{\sqrt{6}}{3}\right)^2=\dfrac{4}{3}\) => C

Câu 4 đề 1:
Biến đổi miền D: \(x^2+y^2\le2x\Leftrightarrow x^2-2x+1+y^2\le1\)
\(\Leftrightarrow\left(x-1\right)^2+y^2\le1\)
Đặt \(\left\{{}\begin{matrix}x-1=r.cos\varphi\\y=r.sin\varphi\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1+r.cos\varphi\\y=r.sin\varphi\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}0\le r\le1\\0\le\varphi\le2\pi\end{matrix}\right.\)
\(I=\int\limits^{2\pi}_0d\varphi\int\limits^1_0\left(2+r.cos\varphi\right).rdr=\int\limits^{2\pi}_0d\varphi\int\limits^1_0\left(2r+r^2.cos\varphi\right)dr\)
\(=\int\limits^{2\pi}_0d\varphi.\left(r^2+\dfrac{r^3}{3}cos\varphi\right)|^1_0=\int\limits^{2\pi}_0\left(1+\dfrac{1}{3}cos\varphi\right)d\varphi=2\pi\)
Câu 4 đề 2: sao câu này người ta ko cho biết chiều tính tích phân nhỉ? Coi như tính theo chiều dương đi.
\(\left\{{}\begin{matrix}P=x^2+xy\\Q=x+2xy\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}P'_y=x\\Q'_x=2y+1\end{matrix}\right.\)
Miền lấy tích phân là miền kín, áp dụng định lý Green:
\(I=\int\limits\int\limits^{ }_D\left(Q'_x-P'_y\right)dxdy=\int\limits\int\limits^{ }_D\left(2y-x+1\right)dxdy\)
Pt AC có dạng \(x=1\) và pt \(BC\) có dạng \(x=3-y\)
Chiếu lên Oy \(\Rightarrow\left\{{}\begin{matrix}0\le y\le2\\1\le x\le3-y\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^2_0dy\int\limits^{3-y}_1\left(2y-x+1\right)dx\)
\(=\int\limits^2_0dy\left(\left(2y+1\right)x-\dfrac{x^2}{2}\right)|^{3-y}_1\)
\(=\int\limits^2_0\left(-\dfrac{5}{2}y^2+6y-2\right)dy=\dfrac{4}{3}\)

\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên

\(A=log_m\left(8m\right)=log_mm+log_m8\)
\(=1+log_m8\)
\(=1+\dfrac{1}{log_8m}=1+\dfrac{1}{log_{2^3}m}=1+\dfrac{1}{\dfrac{1}{3}\cdot log_2m}\)
\(=1+\dfrac{1}{\dfrac{1}{3}a}=1+1:\dfrac{a}{3}=1+\dfrac{3}{a}=\dfrac{a+3}{a}\)
=>Chọn A








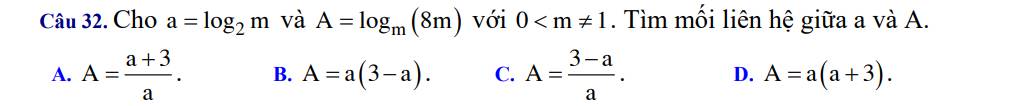

Gọi SH là đường cao của hình chóp, có SH=\(\dfrac{a\sqrt{2}}{2}\) \(\Rightarrow\)\(\widehat{SAH}=45^o\)
Đặt MN=x (x>0), có M'H=\(\dfrac{x\sqrt{2}}{2}\)
Có AMM' là tam giác vuông cân nên AM'=MM' = \(\dfrac{a\sqrt{2}}{2}-\dfrac{x\sqrt{2}}{2}\)
\(V_{MNPQ.M'N'P'Q'}=x^2\left(\dfrac{a\sqrt{2}}{2}-\dfrac{x\sqrt{2}}{2}\right)\)
Giả sử cho a=1 ta có \(V=\dfrac{-x^3\sqrt{2}}{2}+\dfrac{x^2\sqrt{2}}{2}\)
Đạo hàm ta đc \(\dfrac{-3\sqrt{2}x^2}{2}+\sqrt{2}x\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{2}{3}\end{matrix}\right.\)
Vậy MN=\(\dfrac{2a}{3}\)